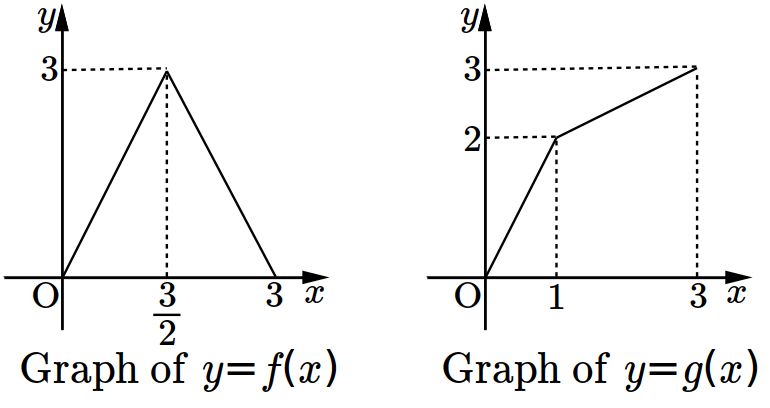
\(A=\log_a \dfrac{x^2}{y^3}\:\) and \(\:B=\log_a\dfrac{y^2}{x^3}\).
Which option is equal to \(3A+2B\)? (※ \(a\ne1\))
- \(\log_a\dfrac{1}{x^5}\)
- \(\log_a\dfrac{1}{y^5}\)
- \(\log_a\dfrac{1}{xy}\)
- \(\log_a\dfrac{x^5}{y^5}\)
- \(\log_a\dfrac{x^5}{y^7}\)