1994 College Scholastic Ability Test No.2

Mathematics·Studies (I)

If \(\sin\theta + \cos\theta= \dfrac{1}{3}\), what is the value of \(\dfrac{1}{\cos\theta}\left(\!\tan\theta+\dfrac{1}{\tan^2\theta}\!\right)\)?

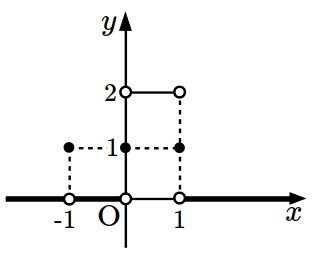
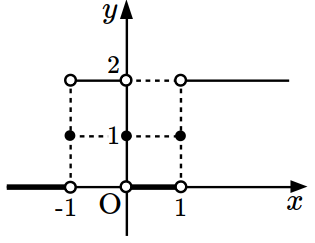
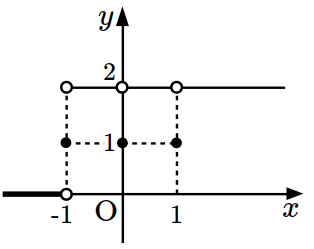
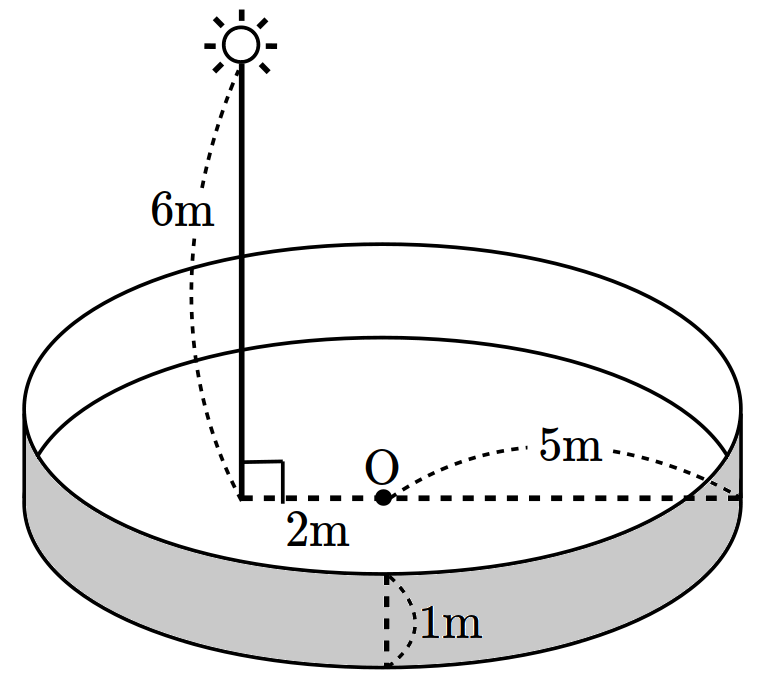
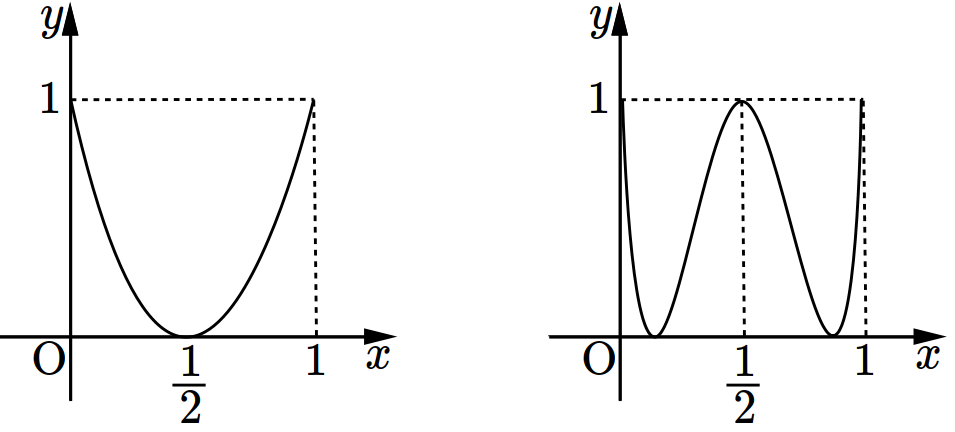\(\dfrac{45}{16}\)
\(\dfrac{43}{16}\)
\(\dfrac{41}{16}\)
\(\dfrac{39}{16}\)
\(\dfrac{37}{16}\)

If two distinct real numbers \(\alpha\) and \(\beta\) satisfy \(\alpha+\beta=1\), what is the value of \(\displaystyle\lim_{x\;\!\to\;\!\infty}\frac{\sqrt{x+\alpha^2}-\sqrt{x+\beta^2}}{\sqrt{4x+\alpha}-\sqrt{4x+\beta}}\)?

\(1\)
\(\dfrac{1}{2}\)
\(2\)
\(\dfrac{1}{4}\)
\(4\)

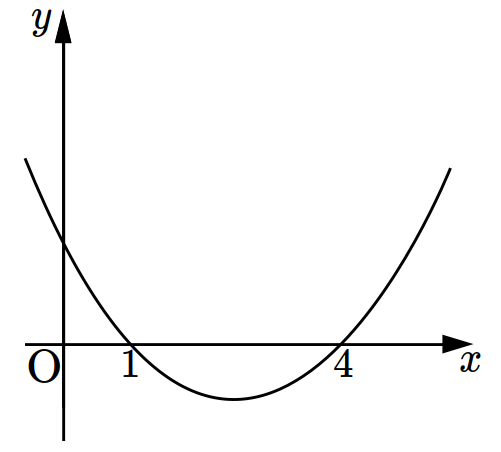
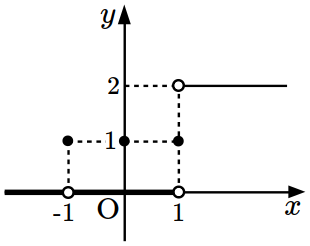
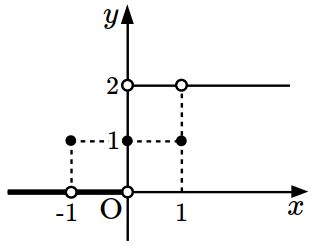
Figure to the right is the graph of \(y=f(x)\). Let the function \(g(x)\) be

\(g(x)=\displaystyle\int_x^{x+1}f(t)dt.\)

What is the minimum value of \(g(x)\)?

\(g(1)\)
\(g(2)\)
\(g\!\left(\!\dfrac{5}{2}\!\right)\)
\(g\!\left(\!\dfrac{7}{2}\!\right)\)
\(g(4)\)

Consider an arithmetic progression with an initial term of \(m\) and a common difference of \(1\). If the sum of the first \(n\) terms of this sequence is \(50\), what is the value of \(m+n\)? (※ \(m\) is a positive integer. \(m \leq 10\).)

\(13\)
\(14\)
\(15\)
\(16\)
\(17\)

Mathematics·Studies (I)

Given that the infinite geometric series \(\displaystyle\sum_{n\;\!=\;\!1}^\infty r^n\) converges, which infinite series below cannot be said to always converge?

\(\displaystyle\sum_{n\;\!=\;\!1}^\infty(r^n+r^{2n})\)
\(\displaystyle\sum_{n\;\!=\;\!1}^\infty(r^n-2r^{2n})\)
\(\displaystyle\sum_{n\;\!=\;\!1}^\infty\frac{r^n+(-r)^n}{2}\)
\(\displaystyle\sum_{n\;\!=\;\!1}^\infty\left(\!\frac{r-1}{2}\!\right)^{\!n}\)
\(\displaystyle\sum_{n\;\!=\;\!1}^\infty\left(\!\frac{r}{2}-1\!\right)^{\!n}\)

The line \(y=3x+2\) translated \(k\) units horizontally, is a tangent line to the parabola \(y^2=4x\).
What is the value of \(k\)?

\(\dfrac{5}{9}\)
\(\dfrac{4}{9}\)
\(\dfrac{2}{9}\)
\(\dfrac{2}{3}\)
\(\dfrac{1}{3}\)

Let the set \(A\) be a subset of the set of all real numbers, such that

if \(x\in A\), then \(\dfrac{1}{2}x\in A\).

Which option below is always correct?

If \(\sqrt{2}\in A\), then \(0 \notin A\).
If \(A\) is a finite set, then \(2 \notin A\).
If \(A\) is an infinite set, then \(0 \in A\).
If \(x\in A\) and \(y \in A\), then \(x+y\in A\).
If \(x\in A\) and \(y \in A\), then \(xy\in A\).

For positive integers \(a\) and \(b\), let \(a◇b\) be the remainder of the division of \(a\) by \(b\). For example,
\(1993◇5=3\). Which option below is incorrect?

\(2^{4n}◇5=1\) for all positive integers \(n\).
\(2^{n}◇5\ne0\) for all positive integers \(n\).
\(2^{m+n}◇5=\{2^m(2^n◇5)\}◇5\)
for all positive integers \(m\) and \(n\).
\(2^{m+n}◇5=\{(2^m◇5)(2^n◇5)\}◇5\)
for all positive integers \(m\) and \(n\).
\((2^m+2^n)◇5=(2^m◇5)+(2^n◇5)\)
for all positive integers \(m\) and \(n\).

Mathematics·Studies (I)

For a \(2 \times 2\) matrix \(A\), what is the list of correct statements in the <List>?
(※ \(E\) is the identity matrix of size \(2\).)

If \(A^3=A^5=E\), then \(A=E\).
If \(A^3+A^2+A+E=O\), then \(A\) is invertible.
If there are three distinct positive integers \(k, m\) and \(n\) such that \(A^k=A^m=A^n=E\), then \(A=E\).

a, b
a, c
b, c
a
c

Consider a cross section of a plane and the cube shown to the right. How many types of shapes can this cross section be among the shapes in the <List>?

A triangle
A rectangle that is not a square
A rhombus that is not a square
A pentagon
A hexagon

\(1\) type
\(2\) types
\(3\) types
\(4\) types
\(5\) types

Let us list the numbers that appear on the figure

to the right in ascending order to create the following sequence.

\(1, 2, 3, 11, 12, 13,\) \(21, 22, 23, 31, 32, 33,\) \(111, 112, 113, 121, \cdots\)

What is the \(200\)th term
of this sequence?

\(13323\)
\(13332\)
\(21111\)
\(21113\)
\(21122\)

Mathematics·Studies (I)

For two distinct integers \(a\) and \(b\), a polynomial \(f(x)\) has the following properties \((\mathrm{A})\) and \((\mathrm{B})\).

\((\mathrm{A})\:\) All coefficients of \(f(x)\) are integers.

\((\mathrm{B})\:\) \(f(a)f(b)=-(a-b)^2\)

The following is a proof that \(\dfrac{f(a)}{a-b}\) is an integer, using the above properties and the following theorem \((\mathrm{C})\).

\((\mathrm{C})\:\) For integers \(m\) and \(n\), if a solution to the quadratic equation \(x^2+mx+n=0\) is a rational number, then that solution is an integer.

(Proof) It is known that \(a^n-b^n\) is divisible by \(a-b\) for all positive integers \(n\). Thus \(f(a)-f(b)\) is divisible by \(a-b\) by the property \((\mathrm{A})\)

ⓐ

.

Therefore, \(\dfrac{f(a)-f(b)}{a-b}\) is an integer.
A quadratic equation with two solutions \(\dfrac{f(a)}{a-b}\) and \(\dfrac{-f(b)}{a-b}\), is \(x^2-\left(\!\dfrac{f(a)-f(b)}{a-b}\!\right)+1=0\), using the relation between solutions and coefficients, and the property \((\mathrm{B})\)

ⓑ

.

\(\dfrac{f(a)}{a-b}\) is a rational number by the property \((\mathrm{A})\)

ⓒ

,

and \(\dfrac{f(a)-f(b)}{a-b}\) is an integer,
so \(\dfrac{f(a)}{a-b}\) is an integer by theorem \((\mathrm{C})\)

ⓓ

Among the underlined parts in the proof above, which part wrongly used either \((\mathrm{A}), (\mathrm{B})\) or \((\mathrm{C})\)?

ⓐ
ⓑ
ⓒ
ⓓ
None.

What is the number of pairs \((a,b)\) where \(a\) and \(b\) are positive integers that satisfy the inequality \(\big|\log_2a-\log_2 10\big|+\log_2b\leq 1\)?

\(15\)
\(17\)
\(19\)
\(21\)
\(23\)

If the product of matrices

\(\begin{pmatrix}x&y\end{pmatrix} \begin{pmatrix}a&b\\b&a\end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}\)

contains a nonnegative number for all real numbers \(x\) and \(y\), what is the minimum value of \(a^2+(b-2)^2\)?

\(1\)
\(\dfrac{1}{2}\)
\(2\)
\(\dfrac{1}{4}\)
\(4\)

Mathematics·Studies (I)

For real numbers \(x\), let \(f(x)\) be the number of real numbers \(t\) that satisfy \(t^2=x^3-x\). Which option below is an appropriate graph of \(y=f(x)\)?

For positive numbers \(a, b\) and \(c\), which option below is a necessary and sufficient condition for the following system of inequalities?

\(\begin{cases} ax^2-bx+c<0\\ cx^2-bx+a<0 \end{cases}\)

\(a+c<\dfrac{b}{2}\)
\(a+c<b\)
\(a+c<2b\)
\(a+c<1\)
\(a+c<2\)

For the function \(f(x)=4x^2-4x+1\:(0\leq x\leq1)\), the graphs of \(y=f(x)\) and \(y=f(f(x))\) are shown below.

What is the number of elements in the set \(\{x\,|\,f(f(f(x)))=x,\:0\leq x\leq1\}\)?

\(16\)
\(12\)
\(8\)
\(6\)
\(5\)

Mathematics·Studies (I)

Consider a doctor. This doctor diagnoses a person having cancer as having cancer with a probability of \(98\%\), and diagnoses a person not having cancer as not having cancer with a probability of \(92\%\). Suppose this doctor examined \(400\) people who actually has cancer and \(600\) people who actually does not have cancer, to diagnose whether they had cancer or not. Suppose one of these \(1000\) people is randomly chosen. What is the probability that the person has been diagnosed as having cancer?

\(39.2\%\)
\(40.0\%\)
\(40.8\%\)
\(44.0\%\)
\(44.8\%\)

A \(1\) meter tall fence surrounds a circular land with a radius of \(5\) meters. Suppose there is a light source \(6\) meters vertically apart from a position on the ground, which is \(2\) meters apart from the center \(\mathrm{O}\) of the circle. What is the area of the shadow of the fence cast by this light source?

\(11\pi\text{m}^2\)
\(14\pi\text{m}^2\)
\(17\pi\text{m}^2\)
\(20\pi\text{m}^2\)
\(24\pi\text{m}^2\)

Consider a moving express train. For the time that the train travels the first \(3\)km, its speed at time \(t\) minutes is \(v(t)=\dfrac{3}{4}t^2+\dfrac{1}{2}t\) (km/minutes), and after that its speed is constant. What is the distance that the train travels for the first \(5\) minutes?

\(17\)km
\(16\)km
\(15\)km
\(14\)km
\(13\)km