1996 College Scholastic Ability Test

Mathematics·Studies (I)

Nat. Sciences

For \(x=2-\sqrt{3}\) and \(y=2+\sqrt{3}\), what is the value of \(\dfrac{y}{x}+\dfrac{x}{y}\)? [1 point]

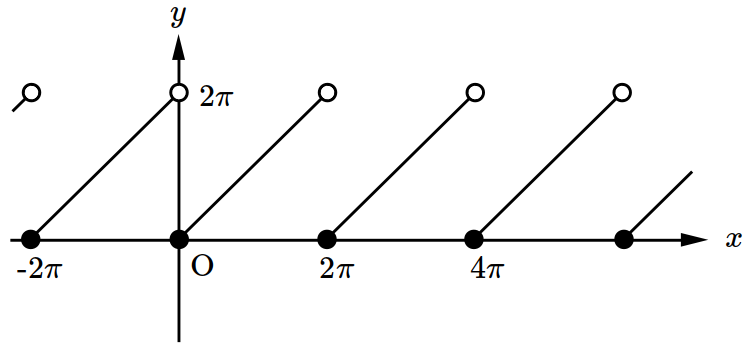
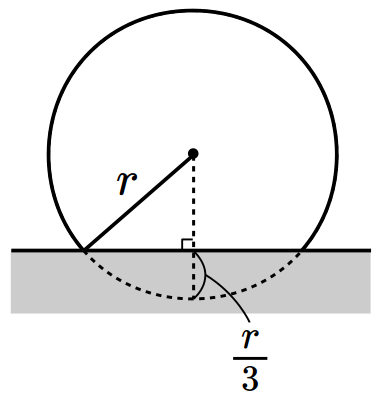
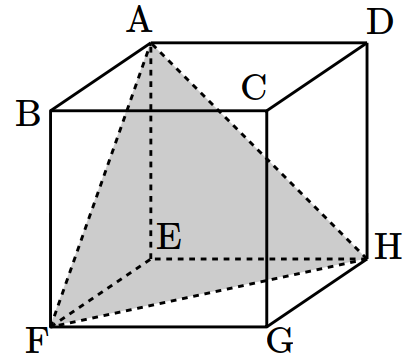
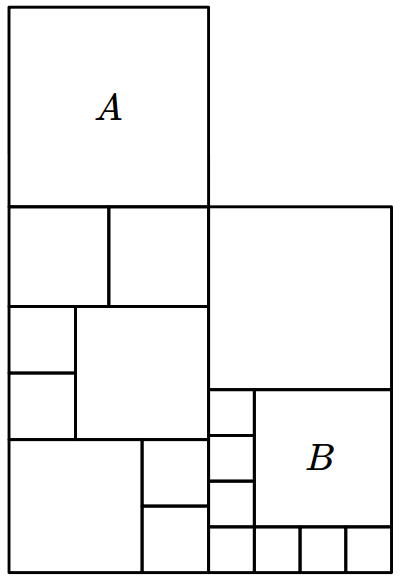
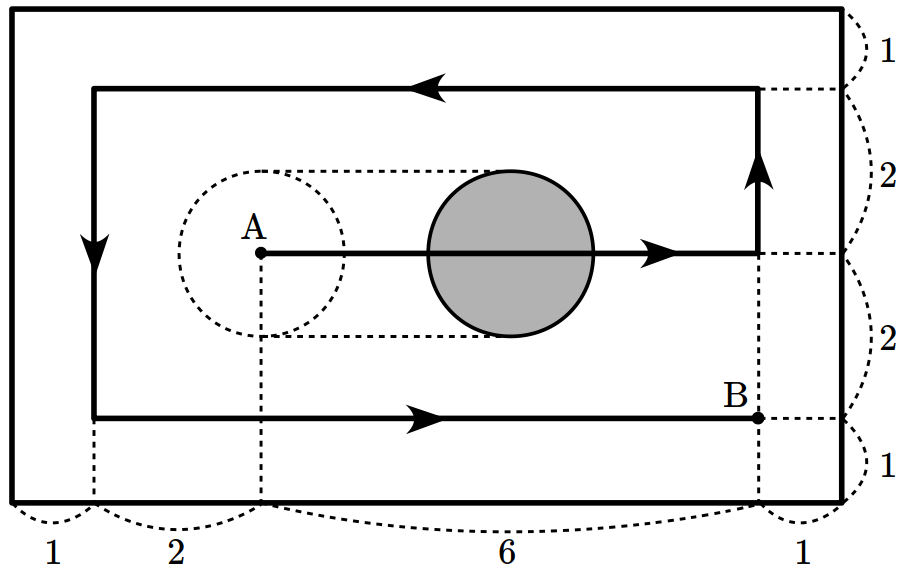
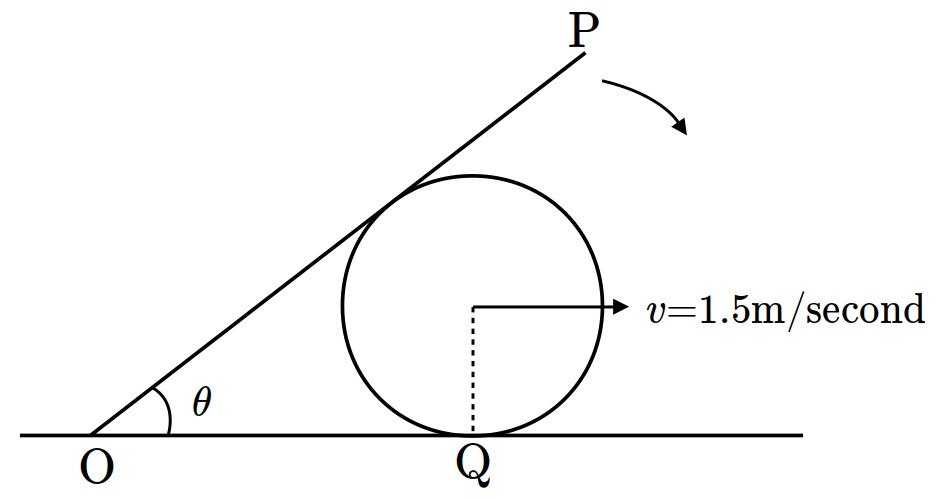
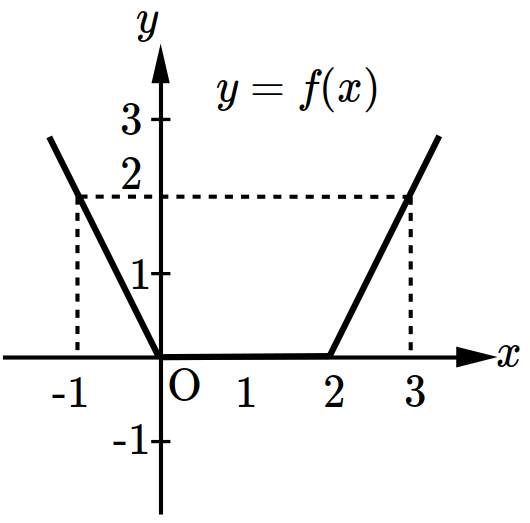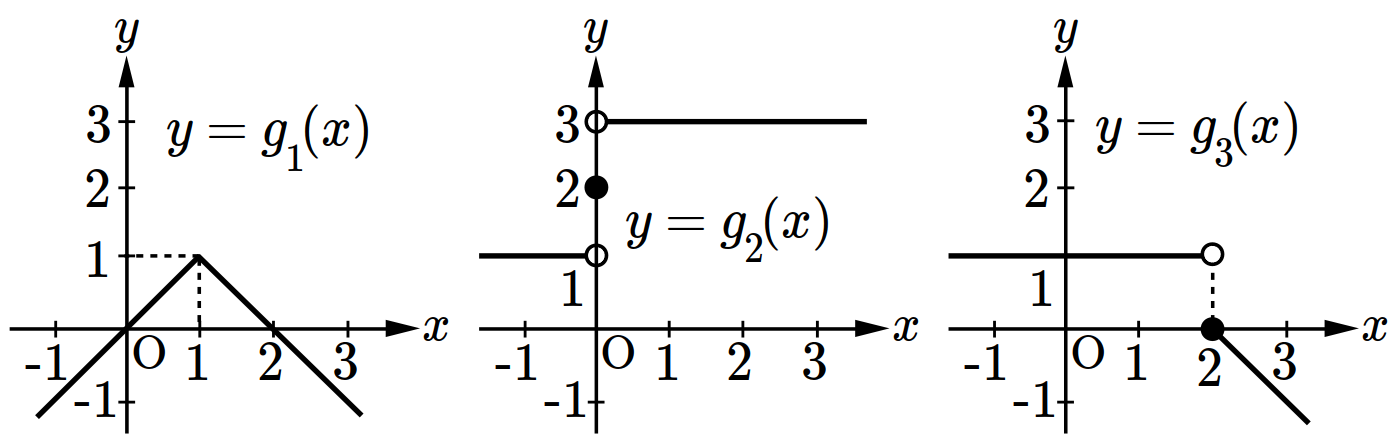\(8\)
\(10\)
\(12\)
\(14\)
\(16\)

The division of the polynomial \(x^4-3x^2+ax+5\) by \(x+2\) has a remainder of \(3\). What is the value of \(a\)? [1 point]

\(0\)
\(2\)
\(3\)
\(-2\)
\(-3\)

For the matrix \(A= \begin{pmatrix*}[r] 1&-1 \\ 0&1 \end{pmatrix*}\), what is the value of \(A^3\)? [1 point]

\(\begin{pmatrix*}[r] 1&-3 \\ 0&1 \end{pmatrix*}\)
\(\begin{pmatrix*}[r] 1&0 \\ -3&1 \end{pmatrix*}\)
\(\begin{pmatrix*}[r] 1&-1 \\ -1&1 \end{pmatrix*}\)
\(\begin{pmatrix*}[r] -1&1 \\ 1&-1 \end{pmatrix*}\)
\(\begin{pmatrix*}[r] 3&-3 \\ 0&3 \end{pmatrix*}\)

What is the value of \(\displaystyle\int_{-1}^{1} |x|e^x dx\)? [1 point]

\(2(e+1)\)
\(2(1-e^{-1})\)
\(2(1-e-e^{-1})\)
\(2(e^{-1}-e)\)
\(2(e+e^{-1})\)

Mathematics·Studies (I)

Nat. Sciences

For \(0 \leq x \leq 2\pi\), what is the number of distinct real solutions to the equation \(\cos^2 x - \sin^2 2x = 0\)? [1 point]

\(3\)
\(4\)
\(5\)
\(6\)
\(7\)

Let \(\mathrm{ABC}\) be a triangle, and consider the statement
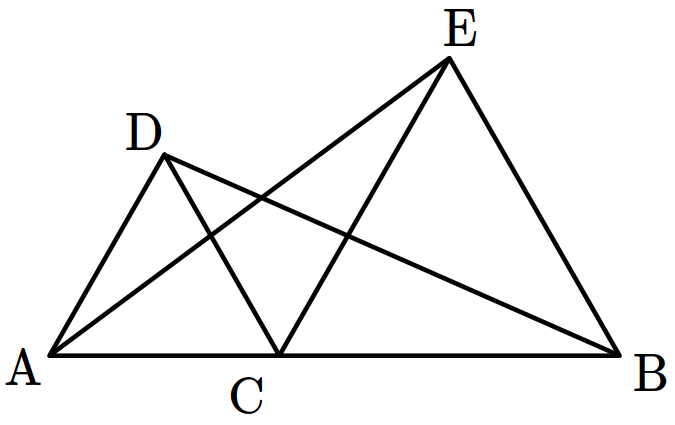
‘If \(\overline{\mathrm{AB}}=\overline{\mathrm{AC}}\), then \(\angle \mathrm{B} = \angle \mathrm{C}\).’ Which option contains all correct statements among the converse, inverse and contrapositive of this statement? [1 point]

Contrapositive
Converse and inverse
Inverse and contrapositive
Converse and contrapositive
Converse, inverse and contrapositive

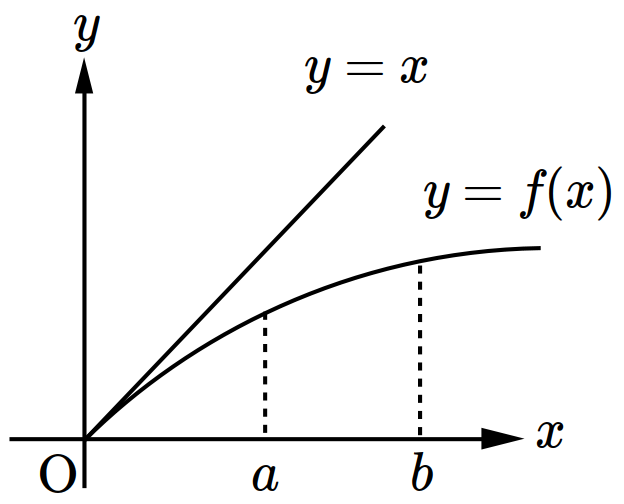
Figure shows the graph of \(y=x\) and a differentiable function \(y=f(x)\). What is the list of correct statements in the <List>, given that \(0<a<b\)? [1 point]

\(\dfrac{f(a)}{a}< \dfrac{f(b)}{b}\)
\(f(b)-f(a) > b-a\)
\(f'(a) > f'(b)\)

a
b
c
a, b
b, c

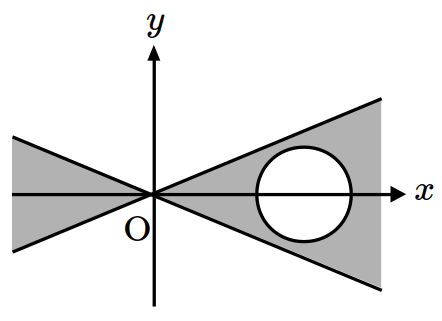
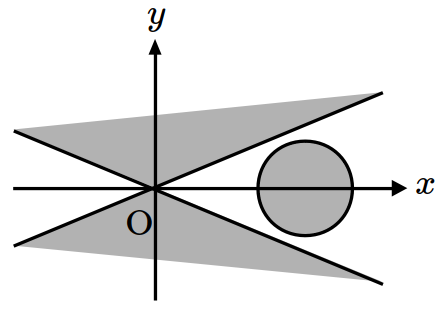
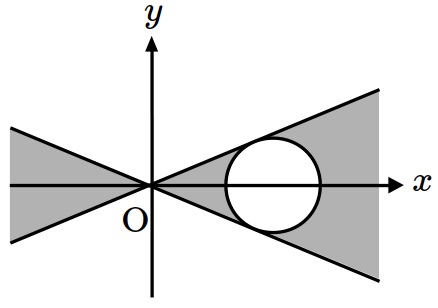
Which option below depicts the region on the
\(xy\)-plane satisfying \((x^2-4y^2)(x^2-6x+y^2+8)\leq 0\)? (※ The boundary of the colored region is included.) [1 point]

Mathematics·Studies (I)

Nat. Sciences

Figure to the right is the graph of a function \(y=f(x)\). Among the functions \(y=g_1(x)\), \(y=g_2(x)\) and \(y=g_3(x)\) shown in the graphs below, which option contains all functions \(g_k(x)\) (\(k=1,2,3\)) such that the function \(y=f(x)g_k(x)\) is continuous on the interval \([-1, 3]\)? [1 point]

\(g_1(x)\)
\(g_2(x)\)
\(g_1(x)\) and \(g_2(x)\)
\(g_1(x)\) and \(g_3(x)\)
\(g_1(x)\), \(g_2(x)\) and \(g_3(x)\)

\(b_k\) equals either \(0\) or \(1\) for \(k=1, 2, 3, 4, \cdots\). If

\(\log_7 2= \dfrac{b_1}{2} + \dfrac{b_2}{2^2} + \dfrac{b_3}{2^3} + \dfrac{b_4}{2^4} + \cdots\),

what are the values of \(b_1, b_2\) and \(b_3\) in this order? [1.5 points]

\(0, 0\) and \(0\)
\(0, 1\) and \(0\)
\(0, 0\) and \(1\)
\(0, 1\) and \(1\)
\(1, 1\) and \(1\)

Consider a right triangle \(\mathrm{ABC}\) with \(\overline{\mathrm{AB}}=2\), \(\overline{\mathrm{BC}}=1\) and \(\angle \mathrm{B}= 90°\). As the figure shows, let \(\mathrm{B_1, B_2, B_3,} \cdots, \mathrm{B}_{n-1}\) be the points dividing the edge \(\mathrm{AB}\) into \(n\) equal parts. Let us draw lines at each point parallel to edge \(\mathrm{BC}\), and let their intersections with edge \(\mathrm{AB}\) be points \(\mathrm{C_1, C_2, C_3,} \cdots, \mathrm{C}_{n-1}\), respectively. What is the value of \(\displaystyle\lim_{n\;\!\to\;\!\infty}\dfrac{2\pi}{n} \displaystyle\sum_{k\;\!=\;\!1}^{n\,-\,1} \overline{\mathrm{B}_k \mathrm{C}_k}^2\)? [1 point]

\(\dfrac{\pi}{6}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{2}\)
\(\dfrac{2\pi}{3}\)
\(\pi\)

Which of the following data has the greatest standard deviation? [1 point]

\(1,5,1,5,1,5,1,5,1,5\)
\(1,5,1,5,1,5,3,3,3,3\)
\(2,4,2,4,2,4,2,4,2,4\)
\(2,4,2,4,2,4,3,3,3,3\)
\(4,4,4,4,4,4,4,4,4,4\)

Mathematics·Studies (I)

Nat. Sciences

In the figure to the right, rectangles \(\mathrm{AODB}\) and \(\mathrm{OFGD}\) are congruent, and rectangles \(\mathrm{BDEC}\) and \(\mathrm{DGHE}\) are congruent. Consider a linear map that maps the point \(\mathrm{B}\) to point \(\mathrm{E}\), and point \(\mathrm{D}\) to point \(\mathrm{A}\). To which point is the point \(\mathrm{A}\) mapped with this linear map? [1.5 points]

\(\mathrm{B}\)
\(\mathrm{C}\)
\(\mathrm{F}\)
\(\mathrm{G}\)
\(\mathrm{H}\)

Below is the graph of the function \(y=f(x)\) defined on all real numbers.

For \(g(x)=\sin x\), which option below is an appropriate graph of the composite function \(y=(g \circ f)(x)\)? [1 point]

Two cars \(A\) and \(B\) are driving in the same direction on a race course shown in the figure. The speed of cars \(A\) and \(B\) are \(a\,\text{km/minutes}\) and \(b\,\text{km/minutes}\) respectively, and the length of one lap around the race course is \(c\,\text{km}\). Given that

\(3a-3b=2c\),

which option below is correct? [1.5 points]

Every \(3\) minutes, \(A\) does two more laps than \(B\).
Every \(3\) minutes, \(A\) does one more lap than \(B\).
Every \(2\) minutes, \(A\) does three more laps than \(B\).
Every \(2\) minutes, \(B\) does two more laps than \(A\).
Every \(2\) minutes, \(B\) does three more laps than \(A\).

A ball with radius \(r\) is floating on still water. As the figure shows, the depth of the ball under the surface is \(\dfrac{r}{3}\). Which expression below is equal to the volume of the part of the ball above the surface? [1.5 points]

\(\pi \displaystyle\int_{\frac{r}{3}}^{2r} (r^2-y^2) dy\)
\(\pi \displaystyle\int_{-\frac{2}{3} r}^{r} (r^2-y^2) dy\)
\(\pi \displaystyle\int_{-\frac{2}{3} r}^{r} (r-y)^2 dy\)
\(\pi \displaystyle\int_{\frac{r}{3}}^{2r} \big(r-\sqrt{r^2-y^2}\big)^2 dy\)
\(\pi \displaystyle\int_{\frac{r}{3}}^{r} \big(r-\sqrt{r^2-y^2}\big)^2 dy\)

Mathematics·Studies (I)

Nat. Sciences

Let us select three random vertices in the cube to the right and form a triangle. What is the number of ways to form a triangle congruent to the triangle shown in the figure? [1.5 points]

\(4\)
\(6\)
\(8\)
\(12\)
\(24\)

The following explains how to produce products \(P_n\) and how much time is required.
(※ \(n=2^k,\: k=0,1,2,3,\cdots\))

A. The time it takes to produce one product \(P_1\) is \(1\).

B. After producing two products \(P_1\), one at a time, you can attach them to produce one product \(P_2\).

C. After producing two products \(P_n\), one at a time, you can attach them to produce one product \(P_{2n}\). The time it takes to attach two products \(P_n\) is \(2n\).

What is the time required to produce one product \(P_{16}\)? [1 point]

\(32\)
\(64\)
\(80\)
\(96\)
\(112\)

Figure below shows some squares attached together. What is the ratio of the edge length of squares \(A\) and \(B\)? [1.5 points]

\(4\,:\,3\)
\(8\,:\,5\)
\(15\,:\,12\)
\(16\,:\,11\)
\(17\,:\,13\)

As the figure shows, let \(\mathrm{C}\) be a point on the line segment \(\mathrm{AB}\), and let us form two equilateral triangles \(\mathrm{ACD}\) and \(\mathrm{BCE}\) above the line segment \(\mathrm{AB}\). The following is a proof that \(\overline{\mathrm{AE}} = \overline{\mathrm{DB}}\).

(Proof)

\(\fbox{\(\;(\alpha)\;\)}\) from triangle \(\mathrm{ACD}\)

\((1)\)

\(\fbox{\(\;(\beta)\;\)}\) from triangle \(\mathrm{BCE}\)

\((2)\)

Since \(\angle \mathrm{ACD} = \angle \mathrm{ECB} = 60°\),

\(\angle \mathrm{ACE} = 60°+ \angle \mathrm{DCE} = \angle \mathrm{DCB}\)

\((3)\)

From \((1), (2)\) and \((3)\),

\(\triangle \mathrm{ACE} \equiv \triangle \mathrm{DCB}\)

since the two sides and the angle between them are equivalent. Therefore \(\overline{\mathrm{AE}} = \overline{\mathrm{DB}}\).

In the proof above, what are appropriate for \((\alpha)\) and \((\beta)\)? [1 point]

	\((\alpha)\)	\((\beta)\)
①	\(\overline{\mathrm{AC}} = \overline{\mathrm{AD}}\)	\(\overline{\mathrm{CE}} = \overline{\mathrm{BE}}\)
②	\(\overline{\mathrm{AC}} = \overline{\mathrm{DC}}\)	\(\overline{\mathrm{CE}} = \overline{\mathrm{BE}}\)
③	\(\overline{\mathrm{AD}} = \overline{\mathrm{CD}}\)	\(\overline{\mathrm{CB}} = \overline{\mathrm{BE}}\)
④	\(\overline{\mathrm{AC}} = \overline{\mathrm{AD}}\)	\(\overline{\mathrm{CE}} = \overline{\mathrm{CB}}\)
⑤	\(\overline{\mathrm{AC}} = \overline{\mathrm{DC}}\)	\(\overline{\mathrm{CE}} = \overline{\mathrm{CB}}\)

Mathematics·Studies (I)

Nat. Sciences

The following is a proof that ‘If \(p\) is even and \(q\) is odd, then the equation \(x^2+px-2q=0\) does not have an integer solution.’

(Proof)
If \(x\) is \(\small\fbox{\(\;(\alpha)\;\)}\), then \(x^2\) is \(\small\fbox{\(\;(\alpha)\;\)}\) and \(px-2q\) is even.
Therefore \(x^2+px-2q\) is \(\small\fbox{\(\;(\alpha)\;\)}\), and thus cannot be \(\small\fbox{\(\;(\beta)\;\)}\).
If \(x\) is \(\small\fbox{\(\;(\gamma)\;\)}\), then \(x^2+px\) is a multiple of \(4\) and \(2q\) is not a multiple of \(4\).
However, this is a contradiction since \(\small\fbox{\(\;(\delta)\;\)}\).
Therefore, this equation does not have an integer solution.

In the proof above, what are appropriate for \((\alpha)\) ~ \((\delta)\)? [1.5 points]

	\((\alpha)\)	\((\beta)\)	\((\gamma)\)	\((\delta)\)
①	even	\(0\)	odd	\(x^2+px=2q\)
②	even	a quadratic equation	odd	\(2q\) is even
③	an integer	\(0\)	even	\(x^2+px=2q\)
④	odd	a quadratic equation	even	\(2q\) is even
⑤	odd	\(0\)	even	\(x^2+px=2q\)

There is a box containing ten balls marked with integers from \(1\) to \(10\). Suppose we mix them well and take two balls out, one by one. The probability that the number marked on the second ball is greater than the first, is \(\dfrac{1}{2}\). The following is a proof of this.
(※ The ball taken out is not put in again)

(Proof)
Let \(X_1\) and \(X_2\) be the numbers marked on the first and second ball respecitvely, and \(p\) be the probability to be calculated. For integers \(n\) from \(1\) to \(10\), let \(A_n\) be the event where \(X_1=n\), and \(B_n\) be the event where \(X_2 \geq n+1\). Then

\(\begin{align} p &= \displaystyle\sum_{n\;\!=\;\!1}^{10} \fbox{\(\;(\alpha)\;\)} \, \cdot \mathrm{P}(A_n) \\ &= \displaystyle\sum_{n\;\!=\;\!1}^{9} \dfrac{10-n}{9} \cdot \fbox{\(\;(\beta)\;\)} \; = \dfrac{1}{2}. \end{align}\)

In the proof above, what are appropriate for \((\alpha)\) and \((\beta)\)? [1.5 points]

	\((\alpha)\)	\((\beta)\)
①	\(\mathrm{P}(A_n \cap B_n)\)	\(\frac{1}{10}\)
②	\(\mathrm{P}(B_n)\)	\(\frac{1}{10}\)
③	\(\mathrm{P}(B_n)\)	\(\frac{1}{9}\)
④	\(\mathrm{P}(B_n \| A_n)\)	\(\frac{9}{10}\)
⑤	\(\mathrm{P}(B_n \| A_n)\)	\(\frac{1}{10}\)

Let \(g(x)\) be the inverse of the function \(f(x) = \dfrac{x^2}{4}+a \,(x\geq 0)\). What is the range of values of \(a\) such that the equation \(f(x)=g(x)\) has two distinct nonnegative solutions? [1.5 points]

\(0 \leq a < 1\)
\(a \geq 0\)
\(a < 1\)
\(0 < a < 2\)
\(a < 2\)

On the complex plane, let \(A\) be the set of points on a ray starting from point \(\mathrm{P}(1)\) passing through \(i\). Let \(B\) be the set of \(5\) distinct complex numbers \(z\) such that \(z^5=1\). What is the number of elements \(z\) in \(B\) such that the product of \(z\) with some element in \(A\) is a real number? (※ \(i=\sqrt{-1}\)) [1.5 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

† This question has been rephrased with the inclusion of \(B\), since the original sentence is hard to translate.

Mathematics·Studies (I)

Nat. Sciences

Consider three points \(\mathrm{A}(0,2)\), \(\mathrm{B}(-1,0)\) and \(\mathrm{C}(1,0)\) on the \(xy\)-plane. Let \(\mathrm{P}\) be a point in \(\triangle \mathrm{ABC}\) or on the boundary of \(\triangle \mathrm{ABC}\), and let \(a, b\) and \(c\) be the distances from point \(\mathrm{P}\) to edges \(\mathrm{AB}, \mathrm{BC}\) and \(\mathrm{CA}\) respectively. Given that \(4b=5(a+c)^2\), what is the shape created by the locus of point \(\mathrm{P}\)? [2 points]

A point
A line segment parallel to the \(x\)-axis
A line segment parallel to the \(y\)-axis
A curve which is a part of a parabola
A curve which is a part of a circle

In \(3\)-dimensional space, consider the circle created by the intersection of two spheres

\(x^2+y^2+z^2=6\) and
\((x-1)^2+(y-2)^2+(z-2)^2=9\).

Let \(\alpha\) be the plane containing this circle, and let \(\theta\) be the angle between plane \(\alpha\) and the \(xy\)-plane. What is the value of \(\cos\theta\)? (※ \(0 \leq \theta \leq \dfrac{\pi}{2}\)) [2 points]

\(\dfrac{1}{3}\)
\(\dfrac{1}{2}\)
\(\dfrac{2}{3}\)
\(\dfrac{\sqrt{3}}{2}\)
\(\dfrac{3}{4}\)

A boat is sailing on a lake from south to north with a constant speed of \(10\,\text{m/second}\). On a bridge built from east to west \(20\,\text{m}\) above the surface of the lake, a car is driving from west to east with a constant speed of \(20\,\text{m/second}\). As the figure shows, currently the boat is \(40\,\text{m}\) south from point \(\mathrm{P}\) on the surface of the lake, and the car is \(30\,\text{m}\) west from point \(\mathrm{Q}\) on the bridge. What is the distance between the boat and the car at the moment when the distance becomes the smallest? (※ Ignore the size of the car and the boat. The line segment \(\mathrm{PQ}\) is perpendicular to the paths of the boat and the car.) [1.5 points]

\(21\,\text{m}\)
\(24\,\text{m}\)
\(27\,\text{m}\)
\(30\,\text{m}\)
\(33\,\text{m}\)

The Mathematics·Studies (I) exam of the College Scholastic Ability Test contains \(30\) questions, and the total score is \(40\) points. The score type of each question can be either \(1\) point, \(1.5\) points, or \(2\) points. Given that there should be at least one question of each score type, what is the minimum number of \(1\) point questions? [1.5 points]

\(8\)
\(9\)
\(10\)
\(11\)
\(12\)

Mathematics·Studies (I)

Nat. Sciences

Figure shows a rectangle with width \(10\) and height \(6\). A circle with radius \(1\) moved inside this rectangle, and the region it passed through was colored with fluorescent paint. The center of the circle moved from point \(\mathrm{A}\) to \(\mathrm{B}\) along the path denoted in the figure with arrows. Given this, what is the area of the region inside the rectangle that is not colored with fluorescent paint? (※ All line segments in the path are parallel to some edge of the rectangle.) [2 points]

\(0\)
\(10 - \dfrac{5}{2}\pi\)
\(8 - 2\pi\)
\(6 - \dfrac{3}{2}\pi\)
\(4 - pi\)

As the figure shows, a stick \(\mathrm{OP}\) is fixed on a point \(\mathrm{O}\) on a flat ground and rests on a circular disk with radius \(1\,\text{m}\). Let \(\mathrm{Q}\) be the point where the disk meets the ground. The center of the disk moves right, parallel to the ground, in a constant speed of \(1.5\,\text{m/second}\). Let \(\theta\) be the angle between the stick \(\mathrm{OP}\) and the ground. When \(\overline{\mathrm{OQ}}=2\,\text{m}\), what is the instantaneous rate of change of \(\theta\) with respect to time? (※ Unit: \(\text{radians/second}\)) [2 points]

\(-\dfrac{3}{5}\)
\(-\dfrac{3}{2}\)
\(-\dfrac{3}{10}\)
\(-\dfrac{\sqrt{5}}{6}\)
\(-\dfrac{3}{2\sqrt{5}}\)