1997 College Scholastic Ability Test

Mathematics·Studies (I)

Nat. Sciences

What is the value of \((125^2-75^2)\div\{5+(30-50)\div(-4)\}\)? [2 points]

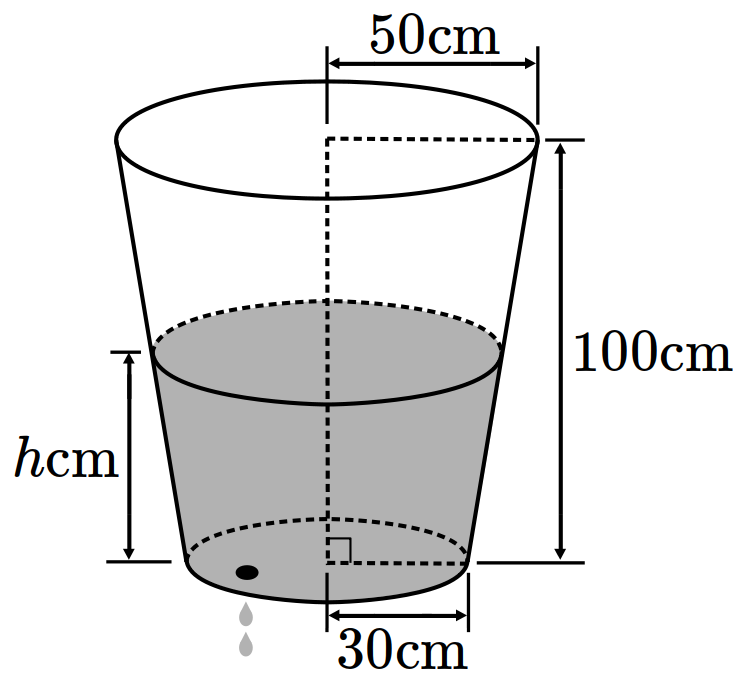
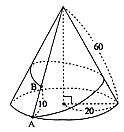
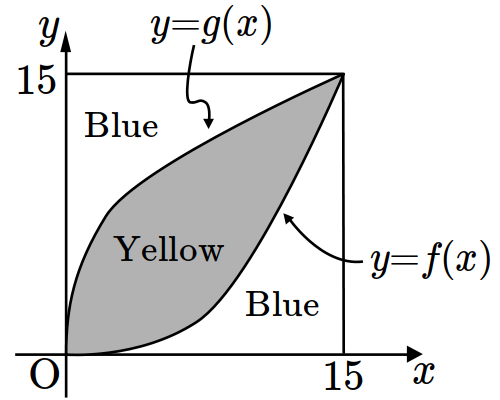
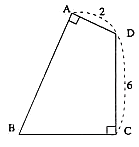
\(75\)
\(125\)
\(900\)
\(1000\)
\(1225\)

For \(\alpha=-2+i\) and \(\beta=1-2i\), what is the value of \(\alpha\overline{\alpha}+\overline{\alpha}\beta+\alpha\overline{\beta}+\beta\overline{\beta}\)? (※ \(\overline{\alpha}\) and \(\overline{\beta}\) are complex conjugates of \(\alpha\) and \(\beta\) respectively. \(i=\sqrt{-1}\).) [2 points]

\(1\)
\(2\)
\(4\)
\(10\)
\(20\)

The angle between two vectors \(\vec{a}\) and \(\vec{b}\) is \(60°\). The magnitude of \(\vec{b}\) is \(1\), and the magnitude of \(\vec{a}-3\vec{b}\) is \(\sqrt{13}\). What is the magnitude of \(\vec{a}\)? [2 points]

\(1\)
\(3\)
\(4\)
\(5\)
\(7\)

What is the value of \(\displaystyle\lim_{x\;\!\to\;\!0}\frac{\sin(3x^3+5x^2+4x)}{2x^3+2x^2+x}\)? [3 points]

\(4\)
\(3\)
\(\dfrac{3}{2}\)
\(1\)
\(\dfrac{\sin3}{2}\)

Mathematics·Studies (I)

Nat. Sciences

Consider the universe \(U\) and its subsets \(A\) and \(B\). Let us define

\(A*B=(A\cap B)\cup(A\cup B)^C\).

Which option below is not always true? (※ \(U\ne\varnothing\)) [2 points]

\(A*U=U\)
\(A*B=B*A\)
\(A*\varnothing=A^C\)
\(A*B=A^C*B^C\)
\(A*A^C=\varnothing\)

Consider a linear map that maps the point \(\mathrm{P}(2,0)\) to point \(\mathrm{Q}\left(\!\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\!\right)\), and the point \(\mathrm{R}(0,2)\) to point \(\mathrm{S}\left(\!-\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\!\right)\). Let \(A\) be the matrix that represents this linear map. Given that \(A^4\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}a\\b\end{pmatrix}\), what is the value of \(\dfrac{a+bi}{1+i}\)? (※ \(i=\sqrt{-1}\)) [2 points]

\(-\dfrac{1}{16}\)
\(\dfrac{\sqrt{2}}{8}\)
\(\dfrac{1}{16}i\)
\(\dfrac{\sqrt{2}+i}{8}\)
\(\dfrac{-1+\sqrt{2}}{16}\)

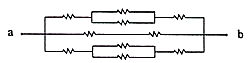
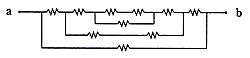
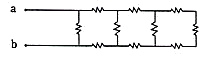
Figure below is a circuit using \(10\) identical resistors (

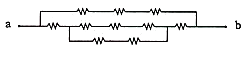
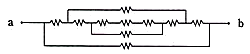
). Which option below has the same topology with this circuit? [2 points]

The annual soft drink sales of some company greatly depends on the average summer temperature of that year. According to past data, the probability of reaching the annual sales quota is
\(0.8\) if the average summer temperature of that year is higher than the previous year,
\(0.6\) if it is about the same as the previous year,
and \(0.3\) if it is lower than the previous year.
According to the weather forecast, the average summer temperature of the next year will be higher than this year with a probability of \(0.4\),
about the same as this year with a probability of \(0.5\),
and lower than this year with a probability of \(0.1\). What is the probability that this company will reach the annual sales quota in the next year? [2 points]

\(0.55\)
\(0.60\)
\(0.65\)
\(0.70\)
\(0.75\)

Mathematics·Studies (I)

Nat. Sciences

Let \(\mathrm{A}(-1,0)\) be a point on the parabola \(y=x(x+1)\). Suppose a point \(\mathrm{P}\) moves along the parabola, starting from point \(\mathrm{A}\), and approaches the origin \(\mathrm{O}\) arbitrarily closely. what is the limit of the magnitude of \(\angle\mathrm{APO}\)? [3 points]

\(90°\)
\(120°\)
\(135°\)
\(150°\)
\(180°\)

A polynomial function \(P(x)\) satisfies the following identity.

\(P(P(x)+x)=(P(x)+x)^2-(P(x)+x)+1\)

What is the value of \(P'(0)\)? [3 points]

\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)

Let \(f(x)\) be a function differentiable on the set of all real numbers, such that

\(f(1-x)=1-f(x)\).

Which option below is not always true? [3 points]

\(f(0)+f(1)=1\)
\(f'(0)=f'(1)\)
\(\displaystyle\int_0^1\!f(x)dx=\frac{1}{2}\)
\(f\!\left(\!\dfrac{1}{2}\!\right)=\dfrac{1}{2}\)
\(f(0)=0\)

Let \(X\) be an absolutely continuous random variable that follows a normal distribution with a mean of \(m\) and a standard deviation of \(\sigma\). It is known that the probability density function of \(X\) is

\(f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\,\large e^{-\small \dfrac{1}{2\sigma^2}(x\,-\,m\,)^2}\) \((-\infty<x<\infty)\).

What is the approximate value of

\(\displaystyle\int_4^{6.6}\sqrt{\frac{2}{\pi}}\,\large e^{-\small \dfrac{(x-5)^2}{8}} \normalsize dx\)

computed with the standard normal table to the right? [2 points]

\(0.1199\)
\(0.3864\)
\(0.6826\)
\(0.9505\)
\(1.9184\)

\(z\)	\(\mathrm{P}(0<Z\leq z)\)
\(\begin{align}0.1\\0.2\\0.3\\0.4\\0.5\\0.6\\0.7\\0.8\\0.9\\1.0\end{align}\)	\(\begin{align}0.0398\\0.0793\\0.1179\\0.1554\\0.1915\\ 0.2257\\0.2580\\0.2881\\0.3159\\0.3413\end{align}\)

Mathematics·Studies (I)

Nat. Sciences

As the figure shows, \(\mathrm{A}\) and \(\mathrm{B}\) runs along a line in the same direction. \(\mathrm{B}\) starts running at the same time with \(\mathrm{A}\), but \(200\) meters ahead of \(\mathrm{A}\).
Let \(a_1\) be the starting position of \(\mathrm{A}\), \(a_2\) be the starting position of \(\mathrm{B}\), \(a_3\) be the position of \(\mathrm{B}\) when \(\mathrm{A}\) reaches \(a_2\), and \(a_4\) be the position of \(\mathrm{B}\) when \(\mathrm{A}\) reaches \(a_3\). Continue this process for all points \(a_n(n=1,2,3,\cdots)\). If the velocity of \(\mathrm{A}\) is \(2\) times the velocity of \(\mathrm{B}\), what is the position of \(\mathrm{A}\) when the distance between \(\mathrm{A}\) and \(\mathrm{B}\) becomes less than a meter for the first time? [3 points]

Between \(a_4\) and \(a_5\)
Between \(a_6\) and \(a_7\)
Between \(a_8\) and \(a_9\)
Between \(a_{10}\) and \(a_{11}\)
Between \(a_{12}\) and \(a_{13}\)

A function \(f(x)\) defined on the set of all real numbers, is a periodic function satisfying \(f(x)=x^2\,(-1\leq x\leq1)\:\) and \(\:f(x+2)=f(x)\).
For all positive integers \(n\), let \(a_n\) be the number of intersections between the line \(y=\dfrac{1}{2n}x+\dfrac{1}{4n}\) and the graph of the function \(y=f(x)\).
What is the value of \(\displaystyle\lim_{n\;\!\to\;\!\infty}\!\frac{a_n}{n}\)? [2 points]

\(0\)
\(1\)
\(2\)
\(3\)
\(4\)

The tangent lines to the parabola \(y=(x-a)^2+b\) at points \(\mathrm{P}(s+a,s^2+b)\) and \(\mathrm{Q}(t+a,t^2+b)\), are perpendicular to each other. Let \(A\) be the area of the shape enclosed by these two tangent lines and the parabola. What is the list of correct statements in the <List>? [2 points]

If \(s\) increases, then \(t\) will increase too.
If \(a\) increases, then \(A\) will increase too.
If \(b\) changes, then \(A\) will change too.

a
b
c
a, c
b, c

† For statement a., assume \(a\) and \(b\) are fixed. For statements b. and c., assume \(s\) and \(t\) are fixed.

Members of the ‘base-\(12\) society’ write integers by using the mapping shown in the table below.

Base-\(10\)	\(1\;\:2\;\:3\;\:4\;\:5\;\:6\;\:7\;\:8\;\:9\;\:10\;\:11\;\:12\;\:13\;\:\cdots\)
Base-\(12\)	\(1\;\:2\;\:3\;\:4\;\:5\;\:6\;\:7\;\:8\;\:9\;\;\:x\;\;\:y\;\:\:\,10\;\:11\;\:\cdots\)

Some examples of addition in base-\(12\) are

\(1+9=x\:\) and \(\:x+y=19\).

Consider two base-\(12\) numbers \(xxx\) and \(yyy\). What is the sum \(xxx+yyy\) written in base-\(12\)? [3 points]

\(1779\)
\(2331\)
\(1xx9\)
\(1yy9\)
\(1yyx\)

Mathematics·Studies (I)

Nat. Sciences

The flowchart to the right is an algorithm finding the smallest positive integer \(n\) such that \(2^{n+1}<9n^4\) is false. What are appropriate for \((\alpha), (\beta)\) and \((\gamma)\) in the flowchart to the right in this order? [2 points]

\(S\!\gets\!S\!+\!2,\;S\geq 9N^4,\:\) Print \(N+1\)
\(S\!\gets\!S\!\times\!2,\;S< 9N^4,\:\) Print \(N\)
\(S\!\gets\!S\!\times\!2,\;S< 9N^4,\:\) Print \(N+1\)
\(S\!\gets\!S\!\times\!2,\;S\geq 9N^4,\:\) Print \(N\)
\(S\!\gets\!S\!\times\!2,\;S\geq 9N^4,\:\) Print \(N+1\)

The following is a part of a proof of the statement ‘If \(x^2+y^2+z^2=1111\), then \(\fbox{\(\;(\alpha)\;\)}\).’

<Proof>
\(\cdots\) (omitted) \(\cdots\)
For the division of integers \(x, y\) and \(z\) by \(8\),
the remainders are either \(0,1,2,3,4,5,6\) or \(7\).
Then, for the division of \(x^2, y^2\) and \(z^2\) by \(8\),
the remainders are either \(0,1\) or \(4\).
Therefore, for the division of \(x^2+y^2+z^2\) by \(8\), the remainder is either \(0,1,2,3,4,5\) or \(6\). However, the division of \(1111\) by \(8\) has a remainder of \(7\).
\(\cdots\) (omitted) \(\cdots\)

What is appropriate for \(\fbox{\(\;(\alpha)\;\)}\) above? [2 points]

at least one of \(x, y\) and \(z\) is an integer.
none of \(x, y\) and \(z\) are integers.
there is at least one solution such that \(x, y\) and \(z\) are all integers.
there is only one solution such that \(x, y\) and \(z\) are all integers.
there are no solutions such that \(x, y\) and \(z\) are all integers.

Figure shows a quadrilateral \(\mathrm{ABCD}\) inscribed in a circle, and the two diagonals \(\mathrm{AC}\) and \(\mathrm{BD}\) meet at point \(\mathrm{P}\) perpendicular to each other. Let \(\mathrm{E}\) be the perpendicular foot from point \(\mathrm{P}\) to edge \(\mathrm{BC}\), and let \(\mathrm{F}\) be the point where the line \(\mathrm{PE}\) meets the edge \(\mathrm{AD}\). Which statement below cannot be proven from this? [3 points]

\(\angle\mathrm{CBP}=\angle\mathrm{PAD}\)
\(\angle\mathrm{APF}=\angle\mathrm{PAF}\)
\(\angle\mathrm{FPD}=\angle\mathrm{FDP}\)
\(\overline{\mathrm{AF}}=\overline{\mathrm{FD}}\)
\(\overline{\mathrm{AP}}=\overline{\mathrm{AF}}\)

What is the minimum distance from a point on the sphere \((x-1)^2+(y-2)^2+(z-3)^2=1\) to the plane \(x+y+z=10\)? [3 points]

\(\dfrac{3\sqrt{3}-3}{3}\)
\(\dfrac{4\sqrt{3}-3}{3}\)
\(\dfrac{3\sqrt{3}+2}{3}\)
\(\dfrac{2\sqrt{3}+5}{3}\)
\(\dfrac{3\sqrt{3}+5}{3}\)

Mathematics·Studies (I)

Nat. Sciences

It is the summer of the year \(2525\), and you are making plans for January \(2526\). You have the calendar of the current year (\(2525\)) from January to December, but you don't have the calendar for the New Year (January \(2526\)). What month in the \(2525\) calendar has the same number of dates, on the same day of the week, as the January \(2526\) calendar? [3 points]

March
May
July
August
No such month.

The electrons of some atom can be in three states \(a,b\) or \(c\) according to the energy. Suppose the following rules hold.

Rule \(1\): If the energy increases, an electron in state \(b\) rises to state \(c\), and an electron in state \(a\) rises to either state \(b\) or state \(c\).

Rule \(2\): If the energy decreases, an electron in state \(b\) falls to state \(a\), and an electron in state \(c\) falls to either state \(b\) or state \(a\).

Suppose an electron is in state \(a\) at <Step \(1\)>. Suppose the energy increases at <Step \(2\)>. Then this electron will rise to state \(b\) or state \(c\). There are \(2\) possible paths this electron can take, namely \(a\;\!\to\;\!b\) and \(a\;\!\to\;\!c\). Suppose the energy decreases again at <Step \(3\)>. There are \(3\) possible paths this electron can take to this point, namely \(a\;\!\to\;\!b\;\!\to\;\!a\), \(a\;\!\to\;\!c\;\!\to\;\!b\), and \(a\;\!\to\;\!c\;\!\to\;\!a\).
If the energy keeps alternately increasing and decreasing in this fashion, what is the number of possible paths this electron can take from <Step \(1\)> to <Step \(7\)>? [3 points]

\(18\)
\(19\)
\(20\)
\(21\)
\(22\)

Figure shows a water tank once completely filled with water, in the shape of a circular cone frustum with a height of \(100\,\text{cm}\), a top radius of \(50\,\text{cm}\), and a base radius of \(30\,\text{cm}\). A hole was made in the base of this water tank and water started to leak. When the height from the base to the surface of the water is \(h\,\text{cm}\), water leaks out with an amount of \(4\sqrt{h}\,\text{cm}^3\) per second. What is the instantaneous rate of change of \(h\) when \(h=50\)?
(Unit: \(\text{cm}/\text{seconds}\)) [4 points]

\(-\dfrac{20\sqrt{2}}{\pi}\times10^{-2}\)
\(-\dfrac{5\sqrt{2}}{\pi}\times10^{-2}\)
\(-\dfrac{20\sqrt{2}}{9\pi}\times10^{-2}\)
\(-\dfrac{5\sqrt{2}}{4\pi}\times10^{-2}\)
\(-\dfrac{4\sqrt{2}}{5\pi}\times10^{-2}\)

† The original image to this question was lost.

Figure shows a mountain in the shape of a right circular cone. A train track is laid along the shortest possible path from point \(\mathrm{A}\) to point \(\mathrm{B}\) which wraps around the mountain once. This track is uphill at first but then becomes downhill. What is the length of the part of the track that is downhill? [4 points]

\(\dfrac{200}{\sqrt{19}}\)
\(\dfrac{300}{\sqrt{30}}\)
\(\dfrac{300}{\sqrt{91}}\)
\(\dfrac{400}{\sqrt{91}}\)
\(\dfrac{500}{\sqrt{91}}\)

† Options \(5\) and \(3\) were identical in the source website due to a typo.

Mathematics·Studies (I)

Nat. Sciences

Short Answers (25~30)

Figure shows a square tile on the \(xy\)-plane with all sides parallel with either the \(x\)-axis or the \(y\)-axis. Suppose we color this tile with blue and yellow, with the graphs of \(y=f(x)\) and \(y=g(x)\) being the boundaries of the colors.
Given that the areas of the region colored blue and the region colored yellow have a ratio of \(2:3\), compute \(\displaystyle\int_0^{15}f(x)dx\).
(※ \(g(x)\) is the inverse of the function \(f(x)\).) [2 points]

Let \(g(x)\) be the inverse of the function

\(f(x)=\begin{cases} \dfrac{71}{5}-\dfrac{19}{15}x & (x<12)\\\\ 1-2\log_3(x-9) & (x\geq12). \end{cases}\)

Compute the value of \(x\) that satisfies \((g\circ g\circ g\circ g\circ g)(x)=-3\).
(※ \((g\circ g)(x)=g\big(g(x)\big)\:\)) [3 points]

As the figure shows, let \(\square \mathrm{ABCD}\) be a quadrilateral whose side lengths are all integers, such that

\(\overline{\mathrm{AD}}=2,\;\overline{\mathrm{CD}}=6,\)
and \(\angle\mathrm{A}=\angle\mathrm{C}=90°\).

Compute the maximum perimeter of this quadrilateral. [3 points]

Let \((a_1,a_2,a_3,a_4)\) be a permutation of the set \(A=\{1,2,3,4\}\). Let \(s_k\,(k=1,2,3)\) be the number of elements to the right of \(a_k\) in the permutation that are less than \(a_k\).
Let us denote the sum \(s_1+s_2+s_3\) as

\(|\,(a_1,a_2,a_3,a_4)\,|\).

For example,

\(\begin{align}|\,(2,4,3,1)\,|\: &=\:s_1+s_2+s_3\\ &=\:1+2+1\:=\:4.\end{align}\)

For all \(24\) permutations \((i_1,i_2,i_3,i_4)\) of the set \(A\), compute the sum of \(|\,(i_1,i_2,i_3,i_4)\,|\). [4 points]

Mathematics·Studies (I)

Nat. Sciences

Polynomial equations \(P(x)=0\) and \(Q(x)=0\) have \(7\) and \(9\) distinct real solutions, respectively,
and the set

\(A=\{(x,y)\,|\,P(x)Q(y)=0\:\) and \(\:Q(x)P(y)=0,\)
\(\qquad\;\; x\) and \(y\) are real numbers\(\}\)

is an infinite set. Let \(B\) be a subset of \(A\) such that

\(B=\{(x,y)\,|\,(x,y)\in A\:\) and \(\:x=y\}\).

Let \(n(B)\) be the number of elements in \(B\). Observe that \(n(B)\) varies according to \(P(x)\) and \(Q(x)\).
Compute the maximum value of \(n(B)\). [4 points]

Using approximations of \(\log_{10}2=0.301\) and \(\log_{10}11=1.041\), compute the value of \(\log_{10}275\), and round the result to the nearest hundredth. [2 points]