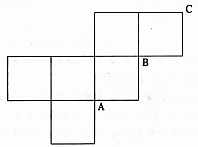
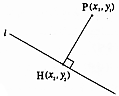
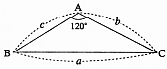
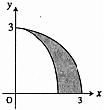
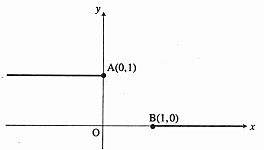
- \(\dfrac{8}{27}\)
- \(\dfrac{16}{81}\)
- \(\dfrac{81}{16}\)
- \(\dfrac{27}{8}\)
- \(\dfrac{64}{81}\)
1998 College Scholastic Ability Test
Mathematics·Studies (I)
Hum. & Arts
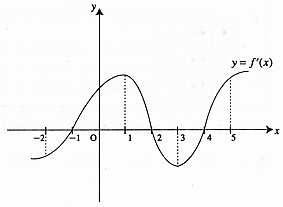
- \(-2\)
- \(-\sqrt{3}\)
- \(1\)
- \(\sqrt{3}\)
- \(2\)
- \(x-1\)
- \(x\)
- \(1\)
- \(x+3\)
- \(3x-1\)
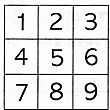
- \(0\)
- \(\dfrac{1}{2}\)
- \(\dfrac{1}{3}\)
- \(\dfrac{1}{4}\)
- \(\dfrac{1}{6}\)
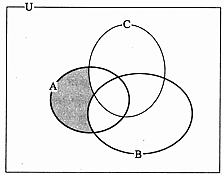
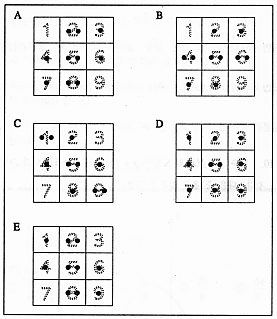
- \(\mathrm{A}\cap(\mathrm{B}\cap \mathrm{C})^C\)
- \(\mathrm{A}\cap(\mathrm{B}\cup \mathrm{C})^C\)
- \(\mathrm{A}\cap(\mathrm{B}^C \cap \mathrm{C})^C\)
- \(\mathrm{A}\cap(\mathrm{B}^C \cap \mathrm{C}^C)^C\)
- \(\mathrm{A}\cap(\mathrm{B}^C \cup \mathrm{C}^C)^C\)