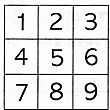
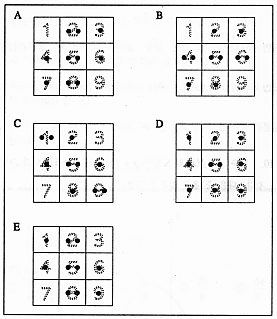
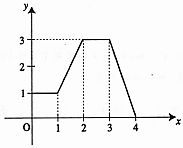
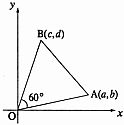
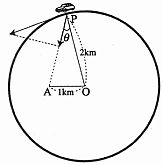
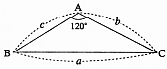
- \(\dfrac{8}{27}\)
- \(\dfrac{16}{81}\)
- \(\dfrac{81}{16}\)
- \(\dfrac{27}{8}\)
- \(\dfrac{64}{81}\)
Mathematics·Studies (I)
Nat. Sciences
- \(y=|x|\)
- \(y=x^2\)
- \(y=\sqrt{x}\)
- \(y=x^3\)
- \(y=\dfrac{1}{x}\)
(※ \(m\) is a constant) [2 points]
- \(3\)
- \(2\)
- \(0\)
- \(-1\)
- \(-3\)
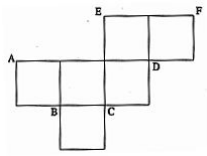
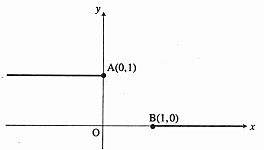
- \(\overrightarrow{\mathrm{CD}}\)
- \(\overrightarrow{\mathrm{DC}}\)
- \(\overrightarrow{\mathrm{ED}}\)
- \(\overrightarrow{\mathrm{DE}}\)
- \(\overrightarrow{\mathrm{FD}}\)
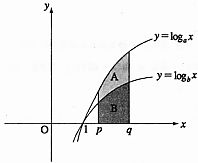
\(x\)-axis, the \(y\)-axis, and the tangent line to the hyperbola \(\dfrac{x^2}{9} - \dfrac{y^2}{16}=1\) at point \((a, b)\)?
(※ \(a>0\) and \(b>0\)) [3 points]
- \(\dfrac{36}{ab}\)
- \(\dfrac{54}{ab}\)
- \(\dfrac{72}{ab}\)
- \(\dfrac{90}{ab}\)
- \(\dfrac{108}{ab}\)
\(\lfloor x \rfloor^2+\lfloor x \rfloor-2=0.\)
Which inequality below has a set of solutions equal to this set?
[3 points]
- \(\dfrac{(x+2)(x-2)}{(x+1)(x-1)}\leq 0\)
- \(\dfrac{(x+1)(x+2)}{(x-1)(x-2)}\leq 0\)
- \(\dfrac{1}{(x+1)(x-1)}\leq 0\)
- \(\dfrac{(x-1)(x+2)}{(x+1)(x-2)}\leq 0\)
- \(\dfrac{(x-2)(x-3)}{(x+2)(x+3)}\leq 0\)