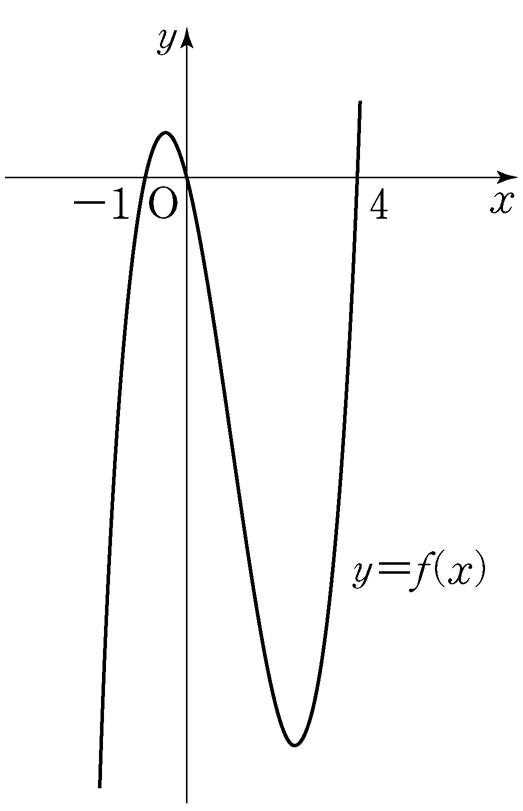
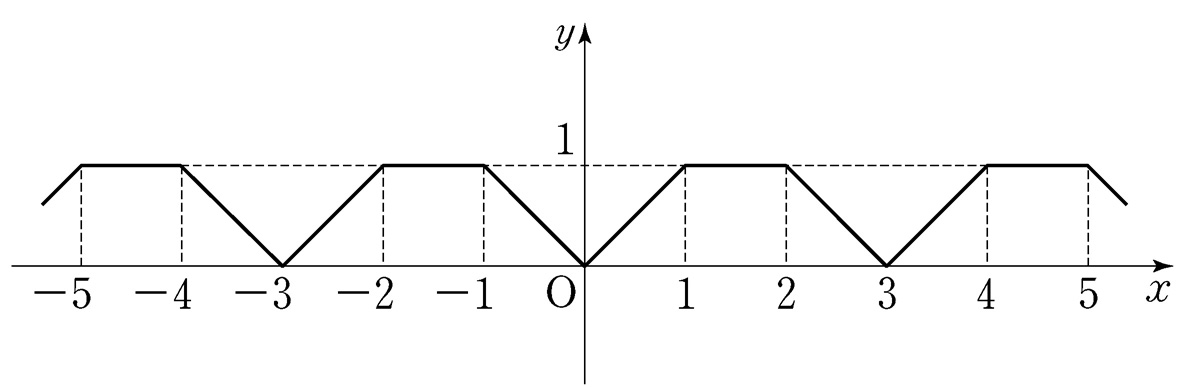
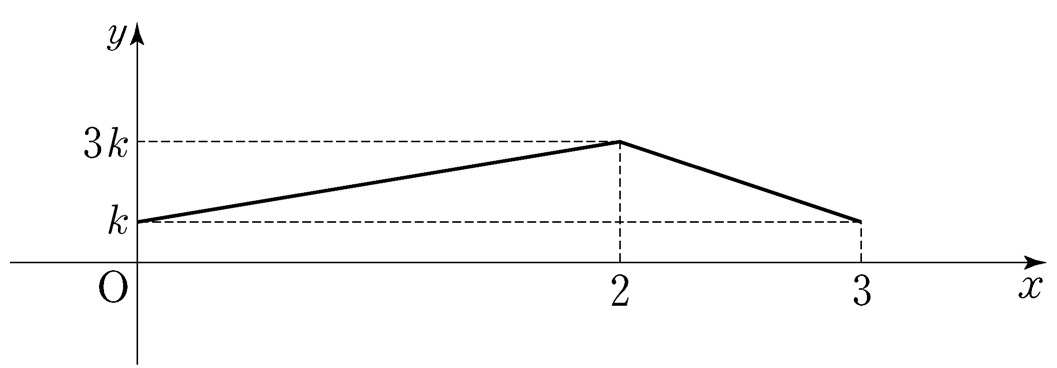
- \(10\)
- \(15\)
- \(20\)
- \(25\)
- \(30\)
2015 College Scholastic Ability Test
Mathematics (Type A)
Multiple Choice Questions
- \(5\)
- \(6\)
- \(7\)
- \(8\)
- \(9\)
- \(1\)
- \(2\)
- \(3\)
- \(4\)
- \(5\)
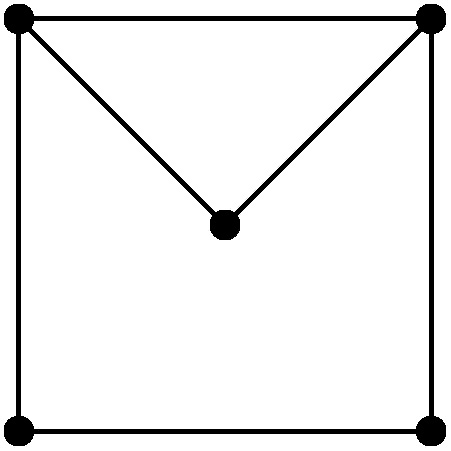
- \(9\)
- \(11\)
- \(13\)
- \(15\)
- \(17\)

| \(z\) | \(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\) |
| \(1.0\) | \(0.3413\) |
| \(1.5\) | \(0.4332\) |
| \(2.0\) | \(0.4772\) |
| \(2.5\) | \(0.4938\) |