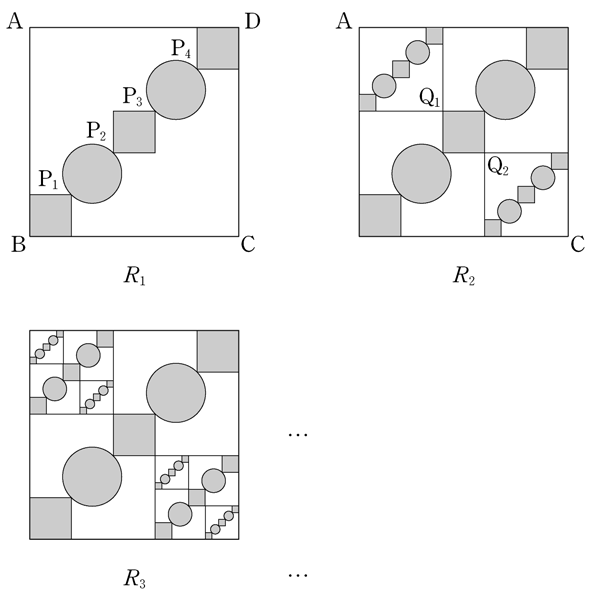
\(a_{n+1} = \dfrac{S_n^2}{S_{n-1}} + (2n-1)S_n \quad (n\geq 2)\)
where \(S_n= \displaystyle\sum_{k\;\!=\;\!1}^{n}a_k\). The following
is a process computing the general term \(a_n\).
Since \(a_{n+1}=S_{n+1}-S_n\), we have
\(S_{n+1} = \dfrac{S_n^2}{S_{n-1}} + 2nS_n \quad (n\geq 2)\).
Dividing both sides with \(S_n\), we have
\(\dfrac{S_{n+1}}{S_n} = \dfrac{S_n}{S_{n-1}}+2n\).
Let \(b_n = \dfrac{S_{n+1}}{S_n}\). Then \(b_1=2\), and
\(b_n=b_{n-1}+2n \quad (n\geq 2)\).
The general term of the sequence \(\{b_n\}\) is
\(b_n = \fbox{\(\;(\alpha)\;\)} \times (n+1) \quad (n\geq 1)\),
therefore
\(S_n =\fbox{\(\;(\alpha)\;\)} \times \{(n-1)!\}^2 \quad (n\geq
1)\).
Therefore \(a_1=1\), and
\(\begin{align} a_n &= S_n-S_{n-1} \\ &= \fbox{\(\;(\beta)\;\)}
\times \{(n-2)!\}^2 \end{align}\)
for \(n\geq 2\).
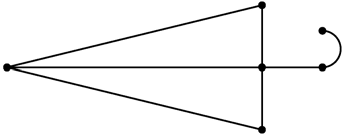

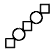 shape.
shape.
 shapes, by
applying the process of obtaining figure \(R_1\) to the newly drawn
two squares respectively.
shapes, by
applying the process of obtaining figure \(R_1\) to the newly drawn
two squares respectively.
 shapes on two
squares with line segments \(\mathrm{AQ_1}\) and \(\mathrm{CQ_2}\) as
a diagonal respectively, using the same process as obtaining figure
\(R_2\) from figure \(R_1\).
shapes on two
squares with line segments \(\mathrm{AQ_1}\) and \(\mathrm{CQ_2}\) as
a diagonal respectively, using the same process as obtaining figure
\(R_2\) from figure \(R_1\).