Let \(N\) be the number of all cases of moving from point \((0,0)\)
to point \((4,3)\) by performing jumps repeatedly. Let \(k\) be the
smallest value that the random variable \(X\) can have. Then
\(k=\fbox{\(\;(\alpha)\;\)}\), and the greatest value that can be
taken is \(k+3\).
\(\mathrm{P}(X=k)=\dfrac{1}{N}\times \dfrac{4!}{3!}=\dfrac{4}{N}\)
\(\mathrm{P}(X=k+1)=\dfrac{1}{N}\times
\dfrac{5!}{2!2!}=\dfrac{30}{N}\)
\(\mathrm{P}(X=k+2)=\dfrac{1}{N}\times \fbox{\(\;(\beta)\;\)}\)
\(\mathrm{P}(X=k+3)=\dfrac{1}{N}\times
\dfrac{7!}{3!4!}=\dfrac{35}{N}\)
and
\(\displaystyle\sum_{i\;\!=\;\!k}^{k+3}\mathrm{P}(X=i)=1\),
therefore \(N=\fbox{\(\;(\gamma)\;\)}\).
Therefore the mean of the random variable \(X\) is
\(\mathrm{E}(X)=\displaystyle\sum_{i\;\!=\;\!k}^{k+3}\{i\times
\mathrm{P}(X=i)\}=\dfrac{257}{43}\).
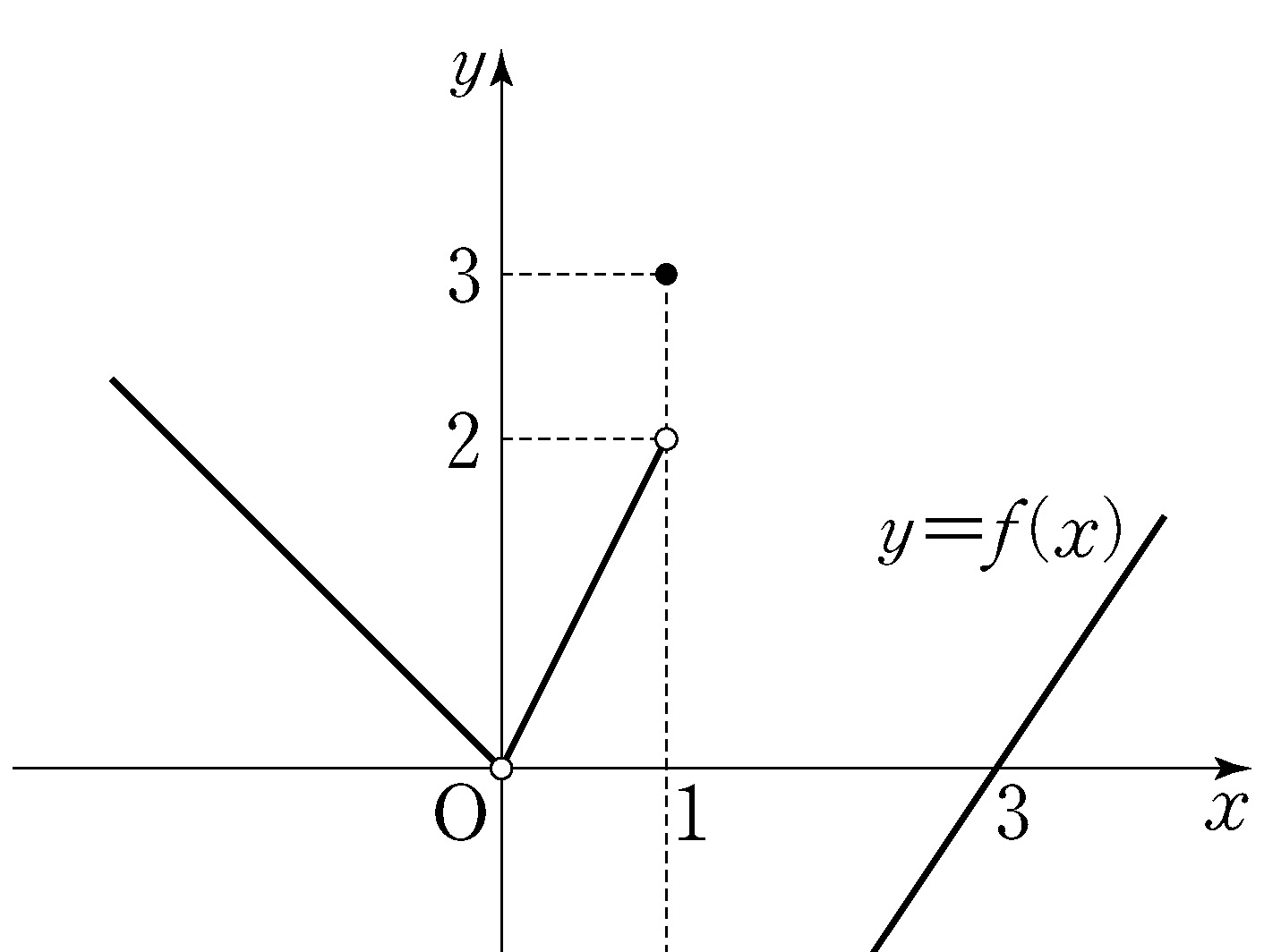
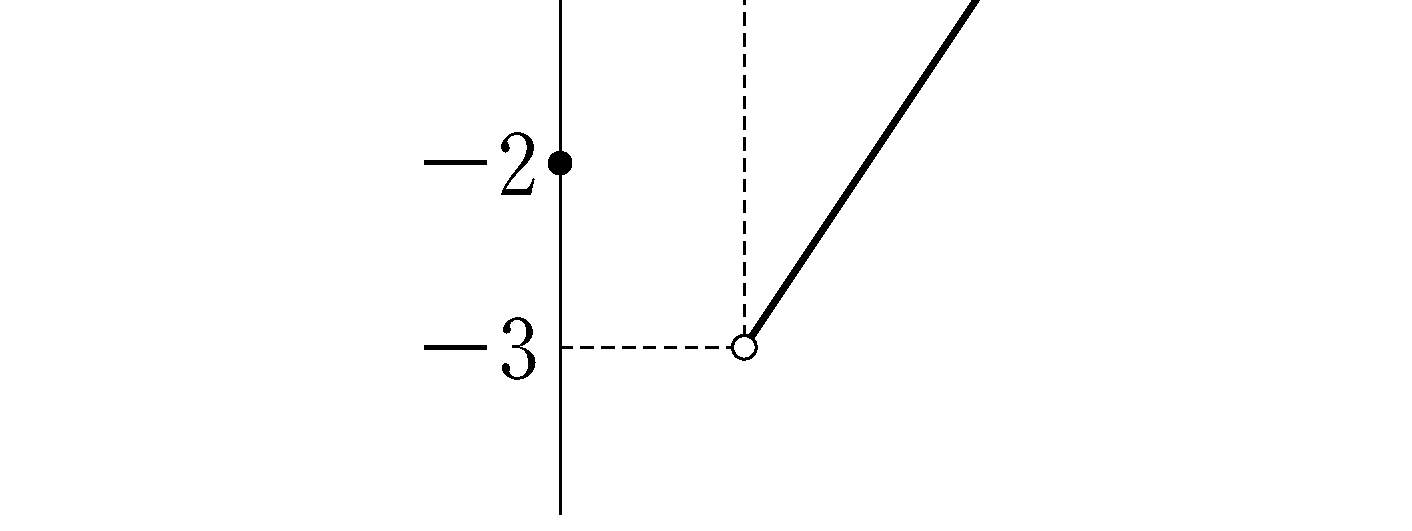
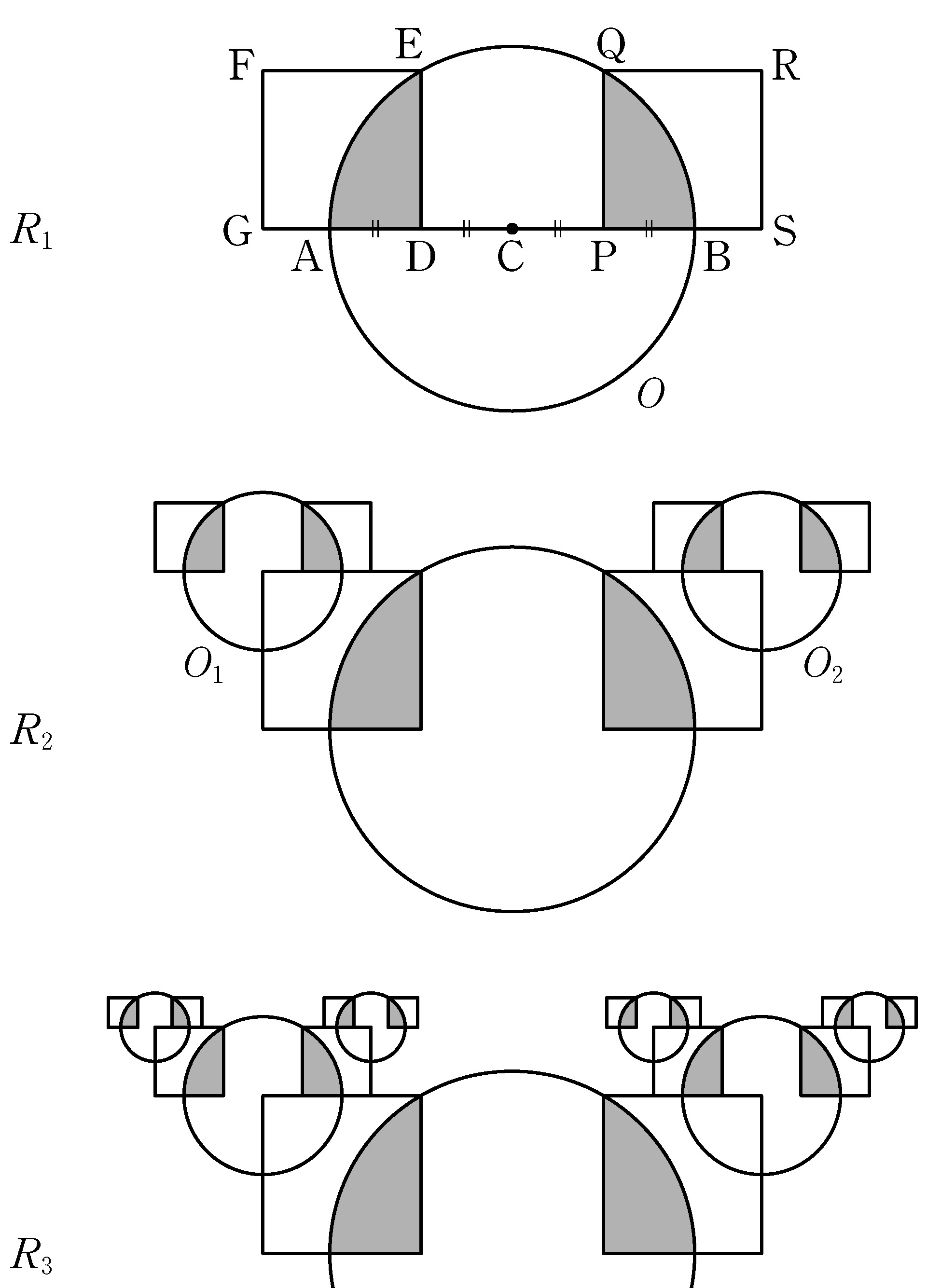
 shape, and the
common region inside circle \(O\) and square \(\mathrm{PQRS}\) with
the
shape, and the
common region inside circle \(O\) and square \(\mathrm{PQRS}\) with
the  shape.
shape.