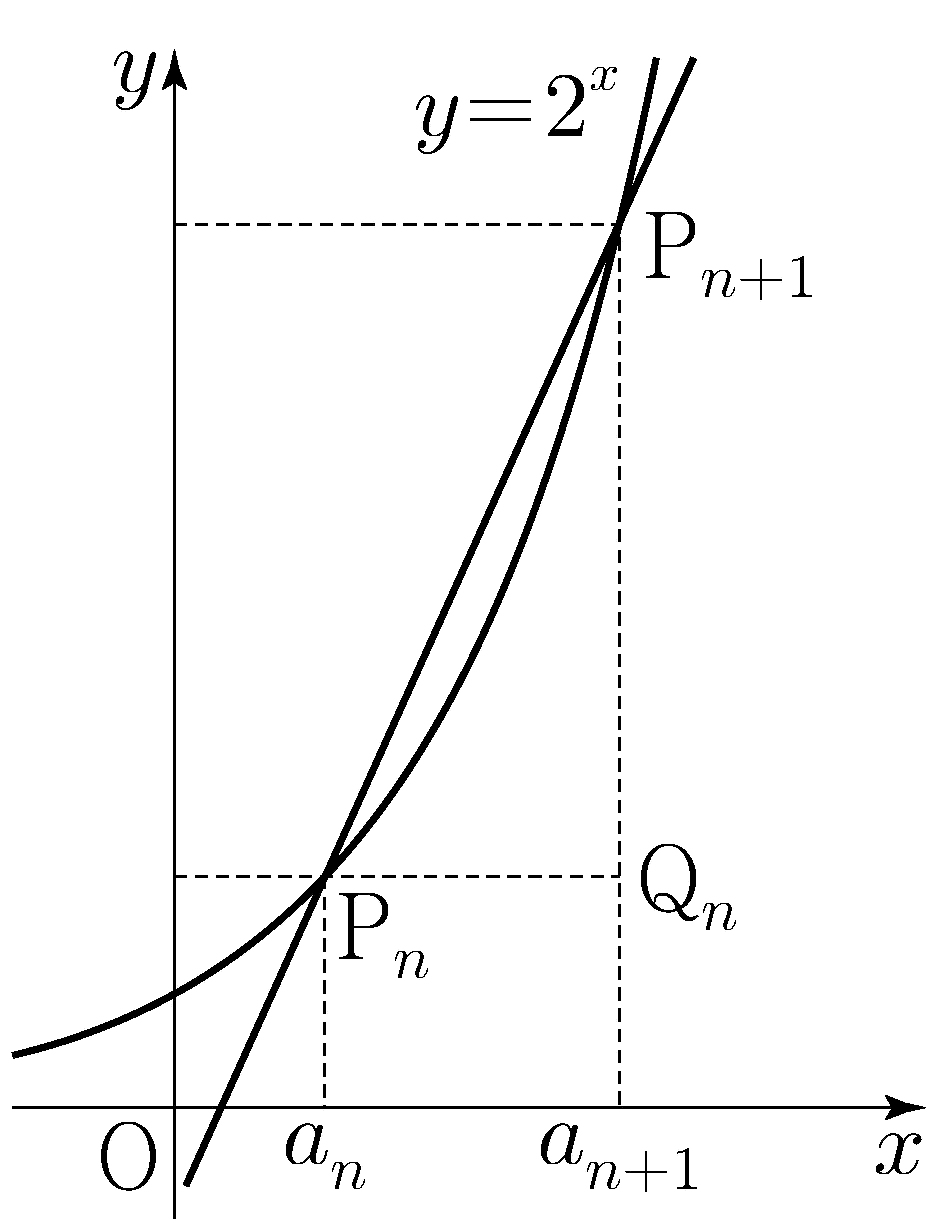
\(a_n<a_{n+1}\), and the line passing through points
\(\mathrm{P}_n\big(a_n,2^{a_n}\big)\) and
\(\mathrm{P}_{n+1}\big(a_{n+1},2^{a_{n+1}}\big)\) has a slope of
\(k\times 2^{a_n}\).
The line passing through points \(\mathrm{P}_n\) and
\(\mathrm{P}_{n+1}\) has a slope of \(k\times 2^{a_n}\), so
\(2^{a_{n+1}-a_n}=k(a_{n+1}-a_n)+1\).
In other words, \(a_{n+1}-a_n\) is a solution to the equation
\(2^x=kx+1\), for all positive integers \(n\).
Since \(k>1\), the equation \(2^x=kx+1\) only has one positive
solution \(d\). Therefore \(a_{n+1}-a_n=d\) for all \(n\), so
\(\{a_n\}\) is an arithmetic progression with a common difference of
\(d\).
Since point \(\mathrm{Q}_n\) has coordinates
\(\big(a_n+1,2^{a_n}\big)\),
\(A_n=\dfrac{1}{2}(a_{n+1}-a_n)\big(2^{a_{n+1}}-2^{a_n}\big)\).
Since \(\dfrac{A_3}{A_1}=16\), we have
\(d=\fbox{\(\;(\alpha)\;\)}\),
so the general term of the sequence \(\{a_n\}\) is
\(a_n=\fbox{\(\;(\beta)\;\)}\).
Therefore \(A_n=\fbox{\(\;(\gamma)\;\)}\) for all positive integers
\(n\).