2023 College Scholastic Ability Test

Mathematics

Multiple Choice Questions

What is the value of \({\left(\!\dfrac{4}{2^\sqrt{2}}\!\right)^{\!2+\sqrt{2}}}\)? [2 points]

\(\dfrac{1}{4}\)
\(\dfrac{1}{2}\)
\(1\)
\(2\)
\(4\)

What is the value of \(\displaystyle\lim_{x\;\!\to\;\!\infty}\!\dfrac{\sqrt{x^2-2}+3x}{x+5}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Let \(\{a_n\}\) be a geometric progression with a positive common ratio such that

\(a_2+a_4=30\:\) and \(\:a_4+a_6=\dfrac{15}{2}\).

What is the value of \(a_1\)? [3 points]

\(48\)
\(56\)
\(64\)
\(72\)
\(80\)

For a polynomial function \(f(x)\), let \(g(x)\) be

\(g(x)=x^2f(x)\).

If \(f(2)=1\) and \(f'(2)=3\), what is the value of \(g'(2)\)? [3 points]

\(12\)
\(14\)
\(16\)
\(18\)
\(20\)

Mathematics

If \(\tan\theta<0\) and \(\cos \!\left(\! \dfrac{\pi}{2}+\theta \right)=\dfrac{\sqrt{5}}{5}\), what is the value of \(\cos\theta\)? [3 points]

\(-\dfrac{2\sqrt{5}}{5}\)
\(-\dfrac{\sqrt{5}}{5}\)
\(0\)
\(\dfrac{\sqrt{5}}{5}\)
\(\dfrac{2\sqrt{5}}{5}\)

The function \(f(x)=2x^3-9x^2+ax+5\) has a local maximum at \(x=1\), and a local minimum at \(x=b\). What is the value of \(a+b\)? (※ \(a\) and \(b\) are constants.) [3 points]

\(12\)
\(14\)
\(16\)
\(18\)
\(20\)

Let \(\{a_n\}\) be an arithmetic progression whose terms are all positive numbers, such that its initial term is equal to its common difference, and

\(\displaystyle\sum_{k\;\!=\;\!1}^{15} \dfrac{1}{\sqrt{a_k}+\sqrt{a_{k+1}}} = 2\).

What is the value of \(a_4\)? [3 points]

\(6\)
\(7\)
\(8\)
\(9\)
\(10\)

Mathematics

What is the \(x\)-intercept of the line that passes through the point \((0,4)\) and is tangent to the curve \(y=x^3-x+2\)? [3 points]

\(-\dfrac{1}{2}\)
\(-1\)
\(-\dfrac{3}{2}\)
\(-2\)
\(-\dfrac{5}{2}\)

Over the closed interval \(\left[-\dfrac{\pi}{6}, b\right]\), the function

\(f(x)=a=\sqrt{3}\tan 2x\)

has a maximum value of \(7\) and a minimum value of \(3\). What is the value of \(a\times b\)? (※ \(a\) and \(b\) are constants.) [4 points]

\(\dfrac{\pi}{2}\)
\(\dfrac{5\pi}{12}\)
\(\dfrac{\pi}{3}\)
\(\dfrac{\pi}{4}\)
\(\dfrac{\pi}{6}\)

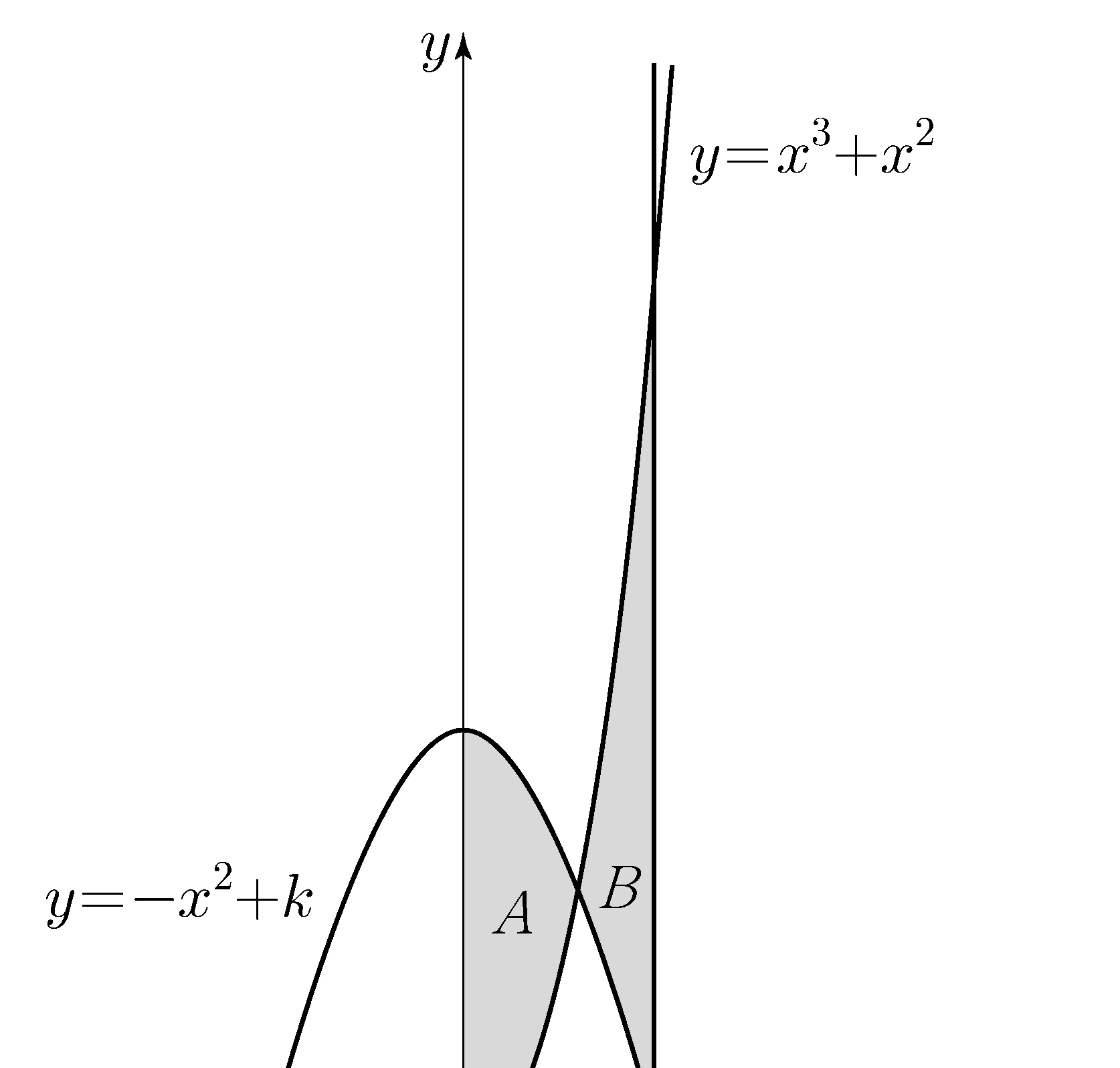
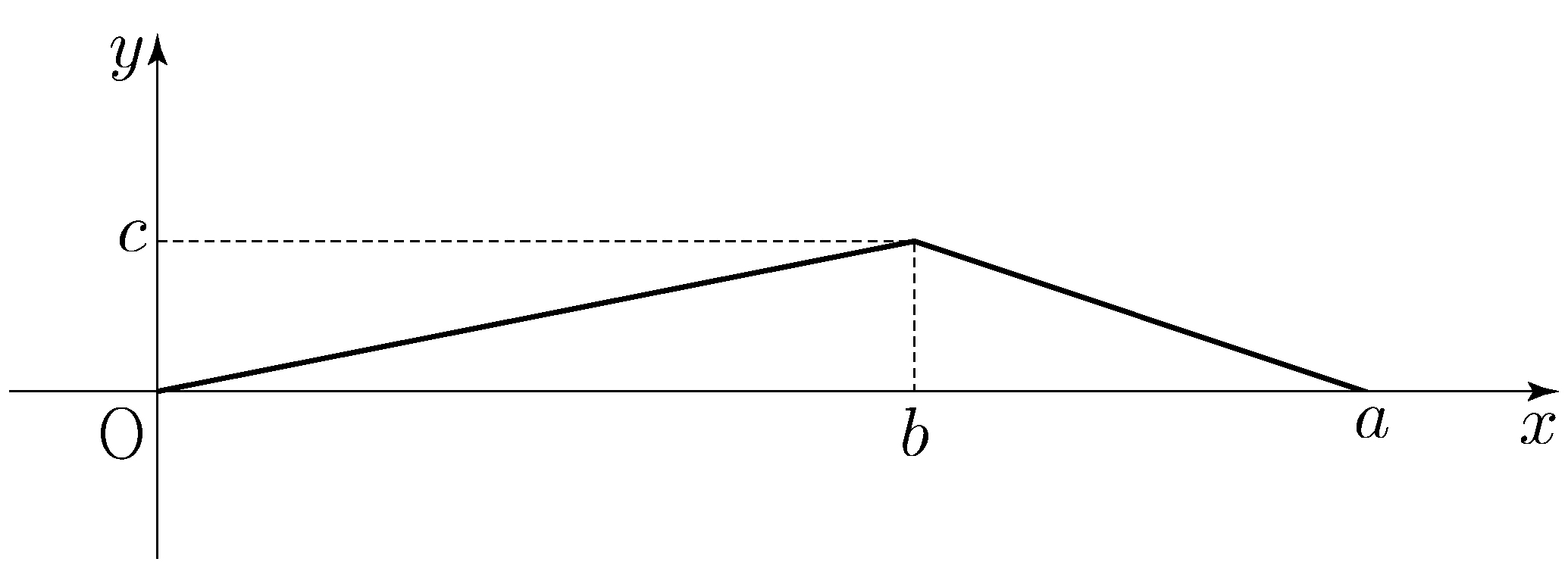
Let \(A\) be the area of the region enclosed by the
\(y\)-axis and two curves \(y=x^3+x^2\) and \(y=-x^2+k\). Let \(B\) be the area of the region enclosed by the line \(x=2\) and two curves \(y=x^3+x^2\) and \(y=-x^2+k\).
If \(A=B\), what is the value of the constant \(k\)?
(※ \(4<k<5\)) [4 points]

\(\dfrac{25}{6}\)
\(\dfrac{13}{3}\)
\(\dfrac{9}{2}\)
\(\dfrac{14}{3}\)
\(\dfrac{29}{6}\)

Mathematics

Figure shows a quadrilateral \(\mathrm{ABCD}\) inscribed in a circle such that

\(\overline{\mathrm{AB}} = 5,\: \overline{\mathrm{AC}} = 3\sqrt{5},\: \overline{\mathrm{AD}} = 7\)
and \(\angle\mathrm{BAC} = \angle\mathrm{CAD}\).

What is the radius of the circle? [4 points]

\(\dfrac{5\sqrt{2}}{2}\)
\(\dfrac{8\sqrt{5}}{5}\)
\(\dfrac{5\sqrt{5}}{3}\)
\(\dfrac{8\sqrt{2}}{3}\)
\(\dfrac{9\sqrt{3}}{4}\)

The function \(f(x)\) is continuous on the set of all real numbers and satisfies the following.

For \(n\!-\!1\leq x \leq n\), \(|f(x)|\!=\!|6(x\!-\!n\!+\!1)(x\!-\!n)|\).
(※ This holds for all positive integers \(n\).)

The function

\(\displaystyle g(x)=\int_0^x \!f(t)dt - \int_x^4 \!f(t)dt\)

defined on the open interval \((0, 4)\), has a minimum value of \(0\) at \(x=2\). What is the value of \(\displaystyle\int_{\begin{array}{c}1 \\\hline 2\end{array}}^4 \!f(x)dx\)? [4 points]

\(-\dfrac{3}{2}\)
\(-\dfrac{1}{2}\)
\(\dfrac{1}{2}\)
\(\dfrac{3}{2}\)
\(\dfrac{5}{2}\)

Mathematics

For all integers \(m \, (m\geq 2)\), let \(f(m)\) be the number of integers \(n \, (n\geq 2)\) such that there exists an integer which is an \(n\)th root of \(m^{12}\).
What is the value of \(\displaystyle\sum_{m\;\!=\;\!2}^9 f(m)\)? [4 points]

\(37\)
\(42\)
\(47\)
\(52\)
\(57\)

For a polynomial function \(f(x)\), let us define the function \(g(x)\) as follows.

\( g(x) = \begin{cases} x & \; (x<-1 \text{ or } x>1)\\ \\ f(x) & \; (-1 \leq x \leq 1) \end{cases} \)

Let \(\displaystyle h(x)\!=\!\lim_{t\;\!\to\;\!0+}\!g(x+t) \!\times\! \lim_{t\;\!\to\;\!2+}\!g(x+t)\). What is the list of correct statements in the <List>? [4 points]

\(h(1)=3\)
\(h(x)\) is continuous on the set of all real numbers.
Suppose \(g(x)\) decreases on the closed interval \([-1,1]\) and \(g(-1)=-2\). Then \(h(x)\) has a global minimum on the set of all real numbers.

a
b
a, b
a, c
b, c

Mathematics

Among all sequences of positive integers \(\{a_n\}\) that satisfy the following condition, let \(M\) and \(m\) be the maximum value and minimum value of \(a_9\) respectively. What is the value of \(M+m\)? [4 points]

\(a_7=40\)
For all positive integers \(n\),
\(a_{n+2} \!=\! \begin{cases} a_{n+1}\!+\!a_n & (a_{n+1}\text{ is not a}\\ & \:\:\text{multiple of }3)\\ \dfrac{1}{3}a_{n+1} & (a_{n+1}\text{ is a multiple of }3). \end{cases} \)

\(216\)
\(218\)
\(220\)
\(222\)
\(224\)

Short Answer Questions

Compute the value of \(x\) such that

\(\log_2 (3x+2) = 2+\log_2 (x-2)\)

is satisfied. [3 points]

Let \(f(x)\) be a function such that \(f'(x)=4x^3-2x\) and \(f(0)=3\). Compute \(f(2)\). [3 points]

Mathematics

Let \(\{a_n\}\) and \(\{b_n\}\) be sequences such that

\(\displaystyle\sum_{k\;\!=\;\!1}^5 (3a_k+5)=55 \:\) and \(\:\displaystyle\sum_{k\;\!=\;\!1}^5 (a_k+b_k)=32\).

Compute \(\displaystyle\sum_{k\;\!=\;\!1}^5 b_k\). [3 points]

Compute the number of integers \(k\) such that the equation \(2x^3-6x^2+k=0\) has \(2\) distinct positive solutions. [3 points]

Consider a point \(\mathrm{P}\) moving on the number line, whose velocity \(v(t)\) and acceleration \(a(t)\) at time \(t\, (t\geq 0)\) satisfy the following.

For \(0\leq t\leq 2\), \(\,v(t)=2t^3-8t\).
For \(t\geq 2\), \(\,a(t)=6t+4\).

Compute the distance that point \(\mathrm{P}\) travels from time \(t=0\) to \(t=3\). [4 points]

Mathematics

Consider a positive integer \(n\). Let us define the function \(f(x)\) as

\( f(x) = \begin{cases} \big|3^{x+2}-n\big| & \; (x < 0)\\ \\ \big|\log_2 (x+4)-n\big| & \; (x \geq 0). \end{cases} \)

For all real numbers \(t\), let \(g(t)\) be the number of distinct real solutions of the equation \(f(x)=t\) (solved for \(x\)). Compute the sum of all positive integers \(n\) for which the maximum value of \(g(t)\) is \(4\). [4 points]

Let \(f(x)\) be a cubic function with a leading coefficient of \(1\), and let \(g(x)\) be a function continuous on the set of all real numbers, such that the following is satisfied. Compute \(f(4)\). [4 points]

\(f(x)=f(1)+(x-1)f'(g(x))\)
for all real numbers \(x\).
The minimum value of \(g(x)\) is \(\dfrac{5}{2}\).
\(f(0)=-3\) and \(f(g(1))=6\).

2023 College Scholastic Ability Test

Mathematics (Prob. & Stat.)

Multiple Choice Questions

In the expansion of the polynomial \((x^3+3)^5\), what is the coefficient of \(x^9\)? [2 points]

\(30\)
\(60\)
\(90\)
\(120\)
\(150\)

Let us pick \(4\) out of the numbers \(1, 2, 3, 4\) and \(5\), such that the same number may be picked multiple times. Let us arrange the picked numbers in a row and make a \(4\)-digit integer. Among all integers that can be made, how many are odd and greater than \(4000\)? [3 points]

\(125\)
\(150\)
\(175\)
\(200\)
\(225\)

Mathematics (Prob. & Stat.)

There is a box containing \(5\) white masks and \(9\) black masks. Let us randomly take out \(3\) masks from this box. What is the probability that at least one of the masks taken out is a white mask? [3 points]

\(\dfrac{8}{13}\)
\(\dfrac{17}{26}\)
\(\dfrac{9}{13}\)
\(\dfrac{19}{26}\)
\(\dfrac{10}{13}\)

There is a sack containing a white ball marked \(1\), a white ball marked \(2\), a black ball marked \(1\), and three black balls marked \(2\). Suppose \(3\) balls are taken out from this sack at the same time. Let \(A\) be the event where \(1\) of them is white and \(2\) of them are black. Let \(B\) be the event where the product of the \(3\) numbers marked on them is \(8\). What is the value of \(\mathrm{P}(A\cup B)\)? [3 points]

\(\dfrac{11}{20}\)
\(\dfrac{3}{5}\)
\(\dfrac{13}{20}\)
\(\dfrac{7}{10}\)
\(\dfrac{3}{4}\)

Mathematics (Prob. & Stat.)

The volume of a shampoo bottle produced in some company follows the normal distribution \(\mathrm{N}(m, \sigma^2)\).
A \(95\%\) confidence interval for \(m\), computed by randomly sampling \(16\) shampoo bottles produced in this company, is \(746.1\leq m\leq 755.9\).
A \(99\%\) confidence interval for \(m\), computed by randomly sampling \(n\) shampoo bottles produced in this company, is \(a\leq m\leq b\). What is the minimum value of \(n\) such that \(b-a\leq 6\)?
(※ The unit of volume is \(\text{mL}\). For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(|Z| \leq 1.96) = 0.95\) and \(\mathrm{P}(|Z| \leq 2.58) = 0.99\).) [3 points]

\(70\)
\(74\)
\(78\)
\(82\)
\(86\)

An absolutely continuous random variable \(X\) takes the value of \(0\leq X\leq a\). The graph of the probability density function of \(X\) is shown below.

Given that \(\mathrm{P}(X\leq b) - \mathrm{P}(X\geq b) = \dfrac{1}{4}\) and \(\mathrm{P}(X\leq \sqrt{5}) = \dfrac{1}{2}\), what is the value of \(a+b+c\)?
(※ \(a, b\) and \(c\) are constants.) [4 points]

\(\dfrac{11}{2}\)
\(6\)
\(\dfrac{13}{2}\)
\(7\)
\(\dfrac{15}{2}\)

Mathematics (Prob. & Stat.)

Short Answer Questions

There are \(6\) cards respectively marked with integers from \(1\) to \(6\) on the front, and all marked with the number \(0\) on the back. Let us place this cards as shown below, such that \(k\) can be seen in the \(k\)th place for all positive integers \(k\leq 6\).

Let us perform the following trial with these \(6\) cards and a die.

Throw the die once, and let \(k\) be the number it lands on. Flip the card in the \(k\)th place and put it back in position.

After repeating the trial above \(3\) times, suppose the sum of the numbers seen on the \(6\) cards is even. Given this, the probability that the die landed on \(1\) exactly once is \(\dfrac{q}{p}\). Compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

For the set \(X=\{x\,|\,x\text{ is an integer, }1 \leq x \leq 10\}\), compute the number of functions \(f:X\;\!\to\;\!X\) that satisfy the following. [4 points]

\(f(x)\leq f(x+1)\)
for all positive integers \(x\leq 9\).
\(f(x)\leq x\) for \(1\leq x \leq 5\), and
\(f(x)\geq x\) for \(6\leq x \leq 10\).
\(f(6)=f(5)+6\)

2023 College Scholastic Ability Test

Mathematics (Calculus)

Multiple Choice Questions

What is the value of \(\displaystyle\lim_{x\;\!\to\;\!0}\dfrac{\ln(x+1)}{\sqrt{x+4}-2}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

What is the value of \(\displaystyle\lim_{n\;\!\to\;\!\infty}\!\dfrac{1}{n}\sum_{k\;\!=\;\!1}^n \sqrt{1+\dfrac{3k}{n}}\)? [3 points]

\(\dfrac{4}{3}\)
\(\dfrac{13}{9}\)
\(\dfrac{14}{9}\)
\(\dfrac{5}{3}\)
\(\dfrac{16}{9}\)

Mathematics (Calculus)

Let \(\{a_n\}\) be a geometric progression such that \(\displaystyle\lim_{n\;\!\to\;\!\infty}\dfrac{a_n+1}{3^n+2^{2n-1}}=3\). What is the value of \(a_3\)? [3 points]

\(16\)
\(18\)
\(20\)
\(22\)
\(24\)

As the figure shows, there is a \(3\)-dimensional solid where one of its faces is the region enclosed by the curve \(y=\sqrt{\sec^2 x+\tan x}\) \(\left(\!0\leq x \leq \dfrac{\pi}{3}\!\right)\), the \(x\)-axis, the \(y\)-axis, and the line \(x=\dfrac{\pi}{3}\). Suppose a cross section of this solid and any plane perpendicular to the \(x\)-axis is always a square. What is the volume of this solid? [3 points]

\(\dfrac{\sqrt{3}}{2}+\dfrac{\ln2}{2}\)
\(\dfrac{\sqrt{3}}{2}+\ln2\)
\(\sqrt{3}+\dfrac{\ln2}{2}\)
\(\sqrt{3}+\ln2\)
\(\sqrt{3}+2\ln2\)

Mathematics (Calculus)

As the figure shows, consider a sector \(\mathrm{OA_1B_1}\) with center \(\mathrm{O}\), radius \(1\) and central angle \(\dfrac{\pi}{2}\). Let \(\mathrm{P_1}\) be a point on arc \(\mathrm{A_1B_1}\), let \(\mathrm{C_1}\) be a point on the line segment \(\mathrm{OA_1}\), and let \(\mathrm{D_1}\) be a point on the line segment \(\mathrm{OB_1}\) such that \(\mathrm{OC_1P_1D_1}\) is a rectangle and \(\overline{\mathrm{OC_1}}:\overline{\mathrm{OD_1}}=3:4\). Let \(\mathrm{Q_1}\) be a point inside the sector \(\mathrm{OA_1B_1}\) such that \(\overline{\mathrm{P_1Q_1}}=\overline{\mathrm{A_1Q_1}}\) and \(\angle\mathrm{P_1Q_1A_1}=\dfrac{\pi}{2}\). Obtain figure \(R_1\) by coloring inside the isosceles triangle \(\mathrm{P_1Q_1A_1}\).
Starting from figure \(R_1\), let \(\mathrm{A_2}\) be a point on the line segment \(\mathrm{OA_1}\) and \(\mathrm{B_2}\) be a point on the line segment \(\mathrm{OB_1}\) such that \(\overline{\mathrm{OQ_1}}=\overline{\mathrm{OA_2}}=\overline{\mathrm{OB_2}}\). Draw a sector \(\mathrm{OA_2B_2}\) with center \(\mathrm{O}\), radius \(\overline{\mathrm{OQ_1}}\) and central angle \(\dfrac{\pi}{2}\). Define four points \(\mathrm{P_2, C_2, D_2}\) and \(\mathrm{Q_2}\) using the same process as figure \(R_1\).
Obtain figure \(R_2\) by coloring inside the isosceles triangle \(\mathrm{P_2Q_2A_2}\). Continue this process, and let \(S_n\) be the area of the colored region in \(R_n\), the \(n\)th obtained figure. What is the value of \(\displaystyle\lim_{n\;\!\to\;\!\infty}S_n\)? [3 points]

\(\dfrac{9}{40}\)
\(\dfrac{1}{4}\)
\(\dfrac{11}{40}\)
\(\dfrac{3}{10}\)
\(\dfrac{13}{40}\)

As the figure shows, consider a point \(\mathrm{C}\) on a semicircle with center \(\mathrm{O}\) and the line segment \(\mathrm{AB}\) as a diameter, such that \(\angle\mathrm{AOC}=\dfrac{\pi}{2}\). Let \(\mathrm{P}\) be a point on arc \(\mathrm{BC}\) and \(\mathrm{Q}\) be a point on arc \(\mathrm{CA}\) such that \(\overline{\mathrm{PB}}=\overline{\mathrm{QC}}\). Let \(\mathrm{R}\) be a point on the line segment \(\mathrm{AP}\) such that \(\angle\mathrm{CQR}=\dfrac{\pi}{2}\). Let \(\mathrm{S}\) be the intersection of line segments \(\mathrm{AP}\) and \(\mathrm{CO}\). For \(\angle\mathrm{PAB}=\theta\), let \(f(\theta)\) be the area of triangle \(\mathrm{POB}\) and \(g(\theta)\) be the area of the quadrilateral \(\mathrm{CQRS}\). What is the value of \(\displaystyle\lim_{\theta\;\!\to\;\!0+}\!\dfrac{3f(\theta)-2g(\theta)}{\theta^2}\)? (※ \(0<\theta<\dfrac{\pi}{4}\)) [4 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Calculus)

Short Answer Questions

For some constants \(a, b\) and \(c\), the function \(f(x)=ae^2x+be^x+c\) satisfies the following.

\(\displaystyle\lim_{x\;\!\to\;\!-\infty}\!\! \dfrac{f(x)+6}{e^x} = 1\)
\(f(\ln 2)=0\)

Let \(g(x)\) be the inverse of \(f(x)\). Given that

\(\displaystyle\int_0^{14}g(x)dx=p+q\ln2\), compute \(p+q\).

(※ \(p\) and \(q\) are rational numbers. \(\ln2\) is irrational.) [4 points]

Let \(f(x)\) be a cubic function with a positive leading coefficient, and let \(g(x)=e^{\sin\pi x}-1\). The composite function \(h(x)=g(f(x))\) defined on the set of all real numbers satisfies the following.

\(h(x)\) has a local maximum value of \(0\) at \(x=0\).
The equation \(h(x)=1\) has \(7\) distinct real solutions in the open interval \((0, 3)\).

Suppose \(f(3)=\dfrac{1}{2}\) and \(f'(3)=0\). Then, \(f(2)=\dfrac{q}{p}\). Compute \(p+q\). (※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

2023 College Scholastic Ability Test

Mathematics (Geometry)

Multiple Choice Questions

Let \(\mathrm{A}(2,2,-1)\) be a point in \(3\)-dimensional space, and \(\mathrm{B}\) be its reflection about the \(x\)-axis. For the point \(\mathrm{C}(-2,1,1)\), what is the length of the line segment \(\mathrm{BC}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

A parabola with focus \(\mathrm{F}\!\left(\!\dfrac{1}{3},0\!\right)\) and directrix \(x=-\dfrac{1}{3}\) passes through point \((a, 2)\). What is the value of \(a\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Geometry)

The tangent line to the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) at point \((2,1)\) on the ellipse, has slope \(-\dfrac{1}{2}\). What is the distance between the two foci of this ellipse?
(※ \(a\) and \(b\) are positive numbers.) [3 points]

\(2\sqrt{3}\)
\(4\)
\(2\sqrt{5}\)
\(2\sqrt{6}\)
\(2\sqrt{7}\)

Consider three vectors

\(\vec{a}=(2,4), \vec{b}=(2,8)\:\) and \(\:\vec{c}=(1,0)\)

on the \(xy\)-plane. Vectors \(\vec{p}\) and \(\vec{q}\) satisfy

\(\big(\vec{p}-\vec{a}\big)\cdot\big(\vec{p}-\vec{b}\big)=0\:\) and \(\:\vec{q}=\dfrac{1}{2}\vec{a}+t\vec{c}\).

What is the minimum value of \(\big|\,\vec{p}-\vec{q}\,\big|\)? [3 points]

\(\dfrac{3}{2}\)
\(2\)
\(\dfrac{5}{2}\)
\(3\)
\(\dfrac{7}{2}\)

Mathematics (Geometry)

Consider a plane \(\alpha\) containing line \(\mathrm{AB}\) in
\(3\)-dimensional space. Consider a point \(\mathrm{C}\) that is not on plane \(\alpha\). Let \(\theta_1\) be the acute angle between line \(\mathrm{AB}\) and line \(\mathrm{AC}\). Suppose \(\sin\theta_1=\dfrac{4}{5}\), and the acute angle between line \(\mathrm{AC}\) and plane \(\alpha\) is \(\dfrac{\pi}{2}-\theta_1\). Let \(\theta_2\) be the acute angle between plane \(\mathrm{ABC}\) and plane \(\alpha\). What is the value of \(\cos\theta_2\)? [3 points]

\(\dfrac{\sqrt{7}}{4}\)
\(\dfrac{\sqrt{7}}{5}\)
\(\dfrac{\sqrt{7}}{6}\)
\(\dfrac{\sqrt{7}}{7}\)
\(\dfrac{\sqrt{7}}{8}\)

Consider a point \(\mathrm{A}\) on the \(y\)-axis, and a hyperbola \(C\) with two foci \(\mathrm{F}(c, 0)\) and \(\mathrm{F'}(-c, 0)\) (\(c>0\)). Let \(\mathrm{P}\) and \(\mathrm{P'}\) be points where the hyperbola \(C\) meets the line segments \(\mathrm{AF}\) and \(\mathrm{AF'}\) respectively. Suppose line \(\mathrm{AF}\) is parallel to an asymptote of the hyperbola \(C\), and suppose

\(\overline{\mathrm{AP}}:\overline{\mathrm{PP'}}=5:6\:\) and \(\overline{\mathrm{PF}}=1\).

What is the length of the major axis of the hyperbola \(C\)? [4 points]

\(\dfrac{13}{6}\)
\(\dfrac{9}{4}\)
\(\dfrac{7}{3}\)
\(\dfrac{29}{12}\)
\(\dfrac{5}{2}\)

Mathematics (Geometry)

Short Answer Questions

Consider a trapezoid \(\mathrm{ABCD}\) on plane \(\alpha\) such that \(\overline{\mathrm{AB}}=\overline{\mathrm{CD}}=\overline{\mathrm{AD}}=2\) and \(\angle\mathrm{ABC}=\angle\mathrm{BCD}=\dfrac{\pi}{3}\). For points \(\mathrm{P}\) and \(\mathrm{Q}\) on plane \(\alpha\) that satisfy the following, compute \(\overrightarrow{\mathrm{CP}}\cdot\overrightarrow{\mathrm{DQ}}\). [4 points]

\(\overrightarrow{\mathrm{AC}}=2\big(\overrightarrow{\mathrm{AD}}+\overrightarrow{\mathrm{BP}}\big)\)
\(\overrightarrow{\mathrm{AC}}\cdot\overrightarrow{\mathrm{PQ}}=6\)
\(2\times\angle\mathrm{BQA}=\angle\mathrm{PBQ}<\dfrac{\pi}{2}\)

Consider a regular tetrahedron \(\mathrm{ABCD}\) in \(3\)-dimensional space. Let \(S\) be a sphere that passes through point \(\mathrm{B}\) with the circumcenter of triangle \(\mathrm{BCD}\) as its center.
Let \(\mathrm{P}\), \(\mathrm{Q}\) and \(\mathrm{R}\) be points where the sphere \(S\) meets the line segments \(\mathrm{AB}\), \(\mathrm{AC}\) and \(\mathrm{AD}\) respectively
(\(\mathrm{P} \ne \mathrm{B}\), \(\mathrm{Q} \ne \mathrm{C}\) and \(\mathrm{R} \ne \mathrm{D}\)).
Let \(\alpha\) be a plane tangent to the sphere \(S\) at point \(\mathrm{P}\). If the radius of sphere \(S\) is \(6\), the projection of triangle \(\mathrm{PQR}\) onto plane \(\alpha\) has an area of \(k\). Compute \(k^2\). [4 points]