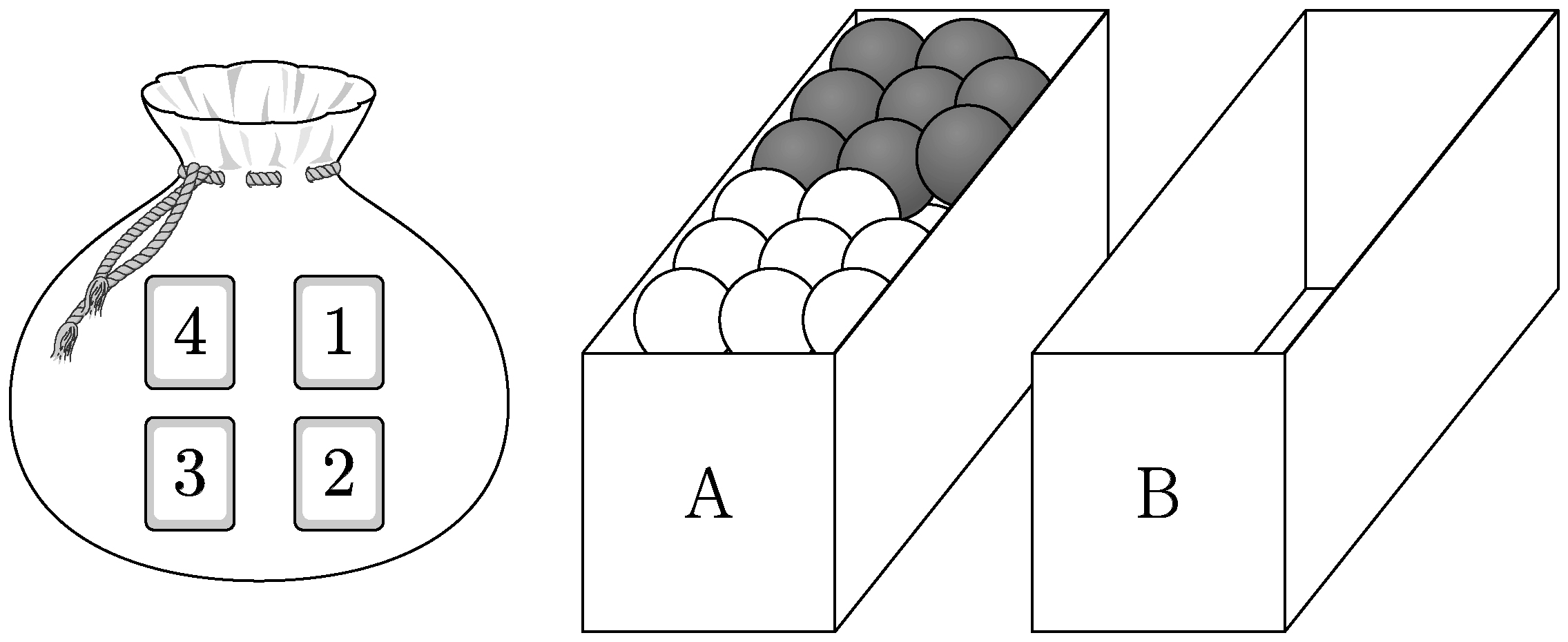
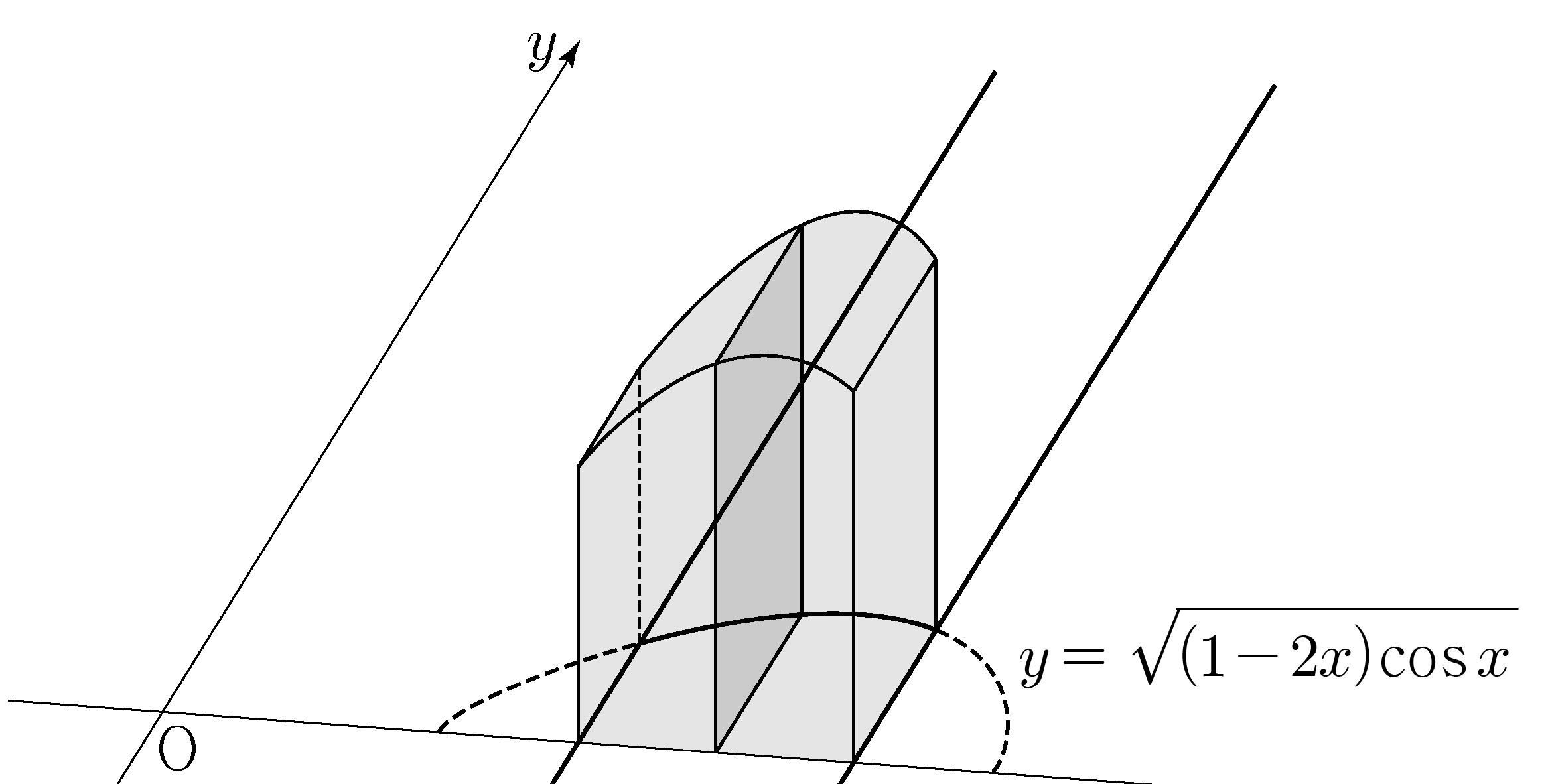
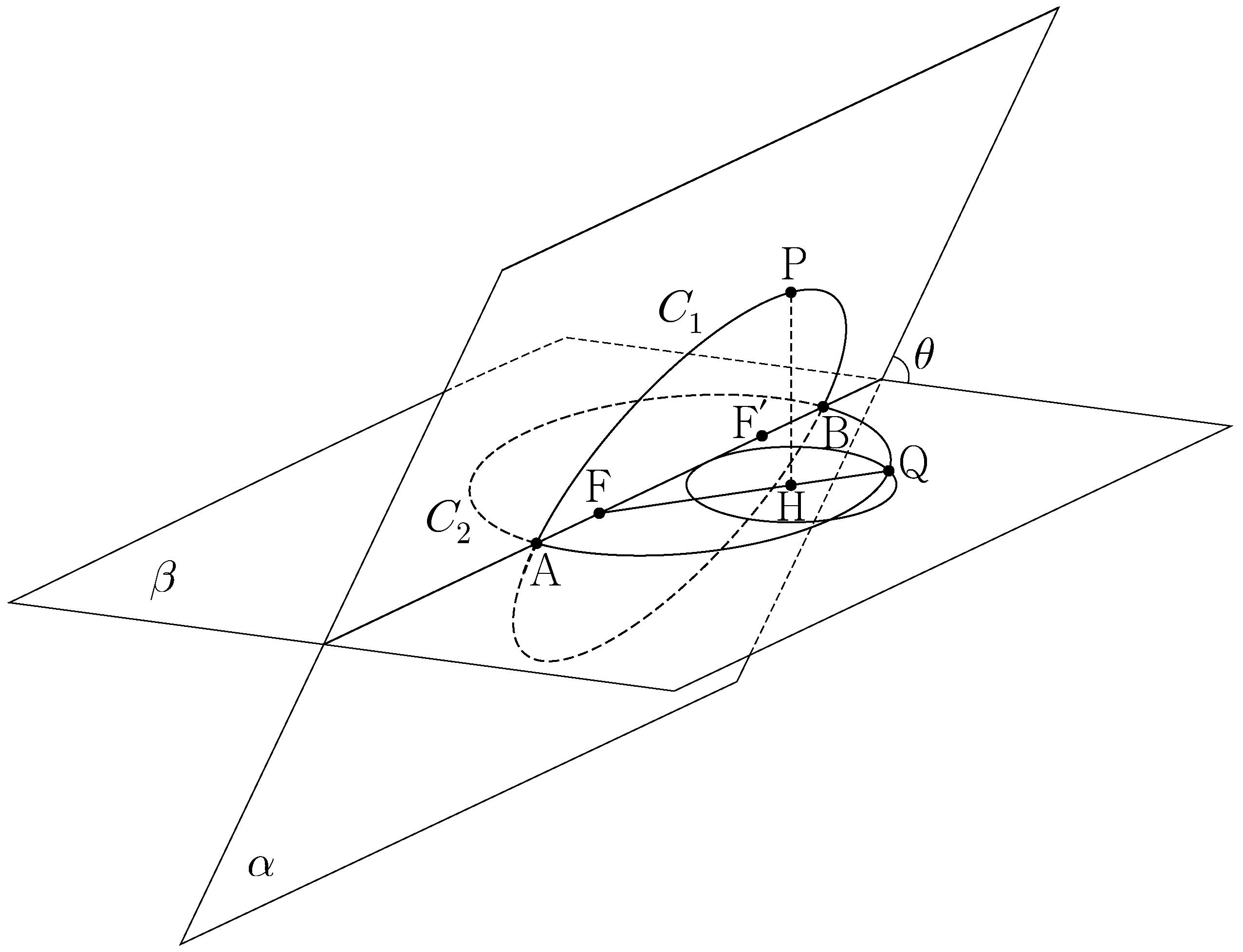
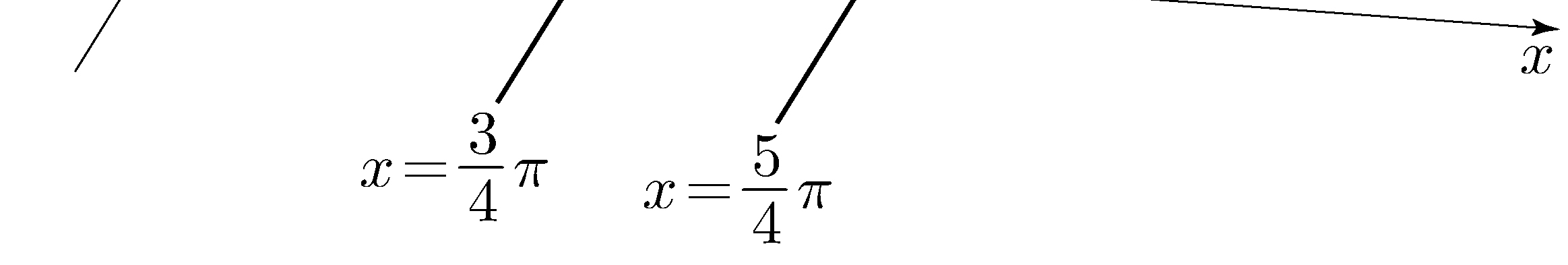- \(6\)
- \(7\)
- \(8\)
- \(9\)
- \(10\)
Mathematics
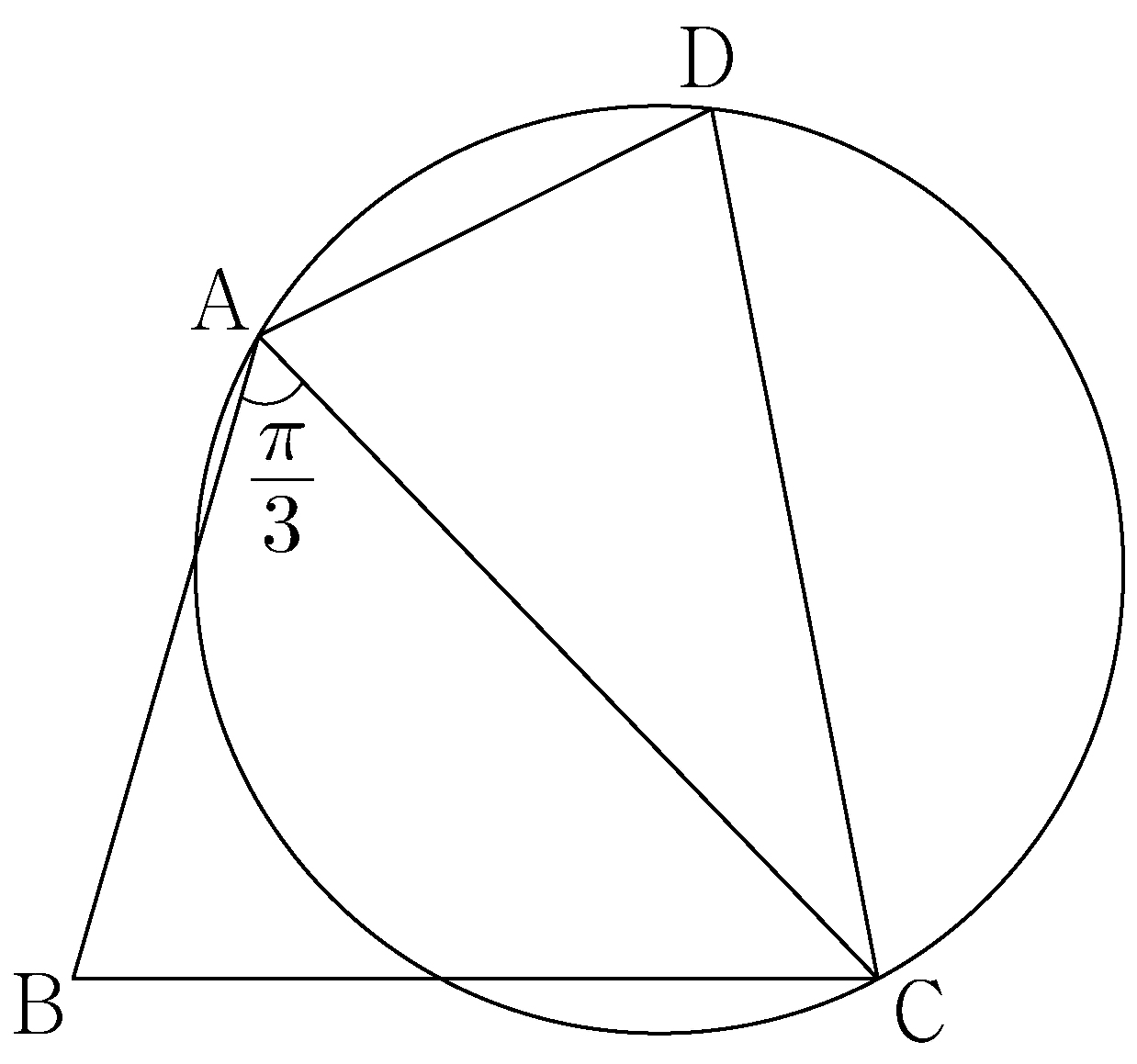
\(\overline{\mathrm{AB}} = 3,\: \overline{\mathrm{BC}} =
\sqrt{13},\: \overline{\mathrm{AD}} \times \overline{\mathrm{CD}} =
9\)
and \(\angle \mathrm{BAC} = \dfrac{\pi}{3}\).
Let \(S_1\) be the area of triangle \(\mathrm{ABC}\), \(S_2\) be the
area of triangle \(\mathrm{ACD}\), and \(R\) be the radius of the
circumcircle of triangle \(\mathrm{ACD}\).
and \(\angle \mathrm{BAC} = \dfrac{\pi}{3}\).
If \(S_2 = \dfrac{5}{6}S_1\), what is the value of \(\dfrac{R}{\sin(\angle \mathrm{ADC})}\)? [4 points]
- \(\dfrac{54}{25}\)
- \(\dfrac{117}{50}\)
- \(\dfrac{63}{25}\)
- \(\dfrac{27}{10}\)
- \(\dfrac{72}{25}\)
\( f(x) = \begin{cases} 2x^3-6x+1 & \; (x \leq 2)\\ \\ a(x-2)(x-b)+9
& \; (x > 2) \end{cases} \)
where \(a\) and \(b\) are positive integers. For real numbers \(t\),
let \(g(t)\) be the number of points where the graph of the function
\(y=f(x)\) meets the line \(y=t\). Suppose there is exactly \(1\) real
number \(k\) such that
\(\displaystyle g(k) + \lim_{t\;\!\to\;\!k-}\!g(t) +
\lim_{t\;\!\to\;\!k+}\!g(t) = 9\).
Among all pairs of positive integers \((a, b)\) that satisfy this
condition, what is the maximum value of \(a+b\)?
[4 points]
- \(51\)
- \(52\)
- \(53\)
- \(54\)
- \(55\)