2025 College Scholastic Ability Test

Mathematics

Multiple Choice Questions

What is the value of \(\sqrt[3]{5} \times 25^{\,\begin{array}{c}1 \\\hline 3\end{array}}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Let \(f(x)=x^3 - 8x + 7\). What is the value of \(\displaystyle\lim_{h\;\!\to\;\!0} \dfrac{f(2+h) - f(2)}{h}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Let \(\{a_n\}\) be a geometric progression whose initial term and common ratio are both \(k\), a positive number. Given that

\(\dfrac{a_4}{a_2} + \dfrac{a_2}{a_1} = 30\),

what is the value of \(k\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

The function

\( f(x) = \begin{cases} 5x+a & \; (x < -2)\\ \\ x^2-a & \; (x \geq -2) \end{cases} \)

is continuous on the set of all real numbers. What is the value of the constant \(a\)? [3 points]

\(6\)
\(7\)
\(8\)
\(9\)
\(10\)

Mathematics

Let \(f(x) = \left(x^2+1\right)\!\left(3x^2-x\right)\).
What is the value of \(f'(1)\)? [3 points]

\(8\)
\(10\)
\(12\)
\(14\)
\(16\)

If \(\cos \left(\dfrac{\pi}{2} + \theta \right) = - \dfrac{1}{5}\), what is the value of \(\dfrac{\sin \theta}{1 - \cos^2 \theta}\)? [3 points]

\(-5\)
\(-\sqrt{5}\)
\(0\)
\(\sqrt{5}\)
\(5\)

Let \(f(x)\) be a polynomial function such that

\(\displaystyle\int_{0}^{x}f(t)dt = 3x^3 + 2x\)

for all real numbers \(x\). What is the value of \(f(1)\)? [3 points]

\(7\)
\(9\)
\(11\)
\(13\)
\(15\)

Mathematics

Let \(a = 2\log_{10} \dfrac{1}{\sqrt{10}} + \log_2 20\:\) and \(\:b = \log_{10}2\).
What is the value of \(a\times b\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Let \(f(x)=3x^2-16x-20\). Given that

\(\displaystyle\int_{-2}^{a} f(x)dx = \int_{-2}^{0} f(x)dx\),

what is the value of the positive number \(a\)? [4 points]

\(16\)
\(14\)
\(12\)
\(10\)
\(8\)

The function \(f(x)=a \cos bx + 3\) defined on the closed interval \([0, 2\pi]\) has a global maximum value of \(13\) at \(x=\dfrac{\pi}{3}\). Among all pairs of positive integers \((a, b)\) that satisfy this condition, what is the minimum value of \(a+b\)? [4 points]

\(12\)
\(14\)
\(16\)
\(18\)
\(20\)

Mathematics

Let \(\mathrm{P}\) be a point moving on the number line, starting from the origin at time \(t=0\). The position of point \(\mathrm{P}\) at time \(t \,(t \geq 0)\) is

\(x = t^3 - \dfrac{3}{2}t^2 - 6t\).

What is the acceleration of point \(\mathrm{P}\) at the time when it changes its direction of motion? [4 points]

\(6\)
\(9\)
\(12\)
\(15\)
\(18\)

Let \(\{a_n\}\) be a sequence with \(a_1=2\), and let \(\{b_n\}\) be an arithmetic progression with \(b_1=2\), such that

\(\displaystyle\sum_{k\;\!=\;\!1}^{n} \dfrac{a_k}{b_{k+1}} = \dfrac{1}{2} n^2\)

for all positive integers \(n\).
What is the value of \(\displaystyle\sum_{k\;\!=\;\!1}^{5}a_k\)? [4 points]

\(120\)
\(125\)
\(130\)
\(135\)
\(140\)

Mathematics

Let \(f(x)\) be a cubic function with a leading coefficient of \(1\) such that

\(f(1)=f(2)=0\,\) and \(\,f'(0) = -7\).

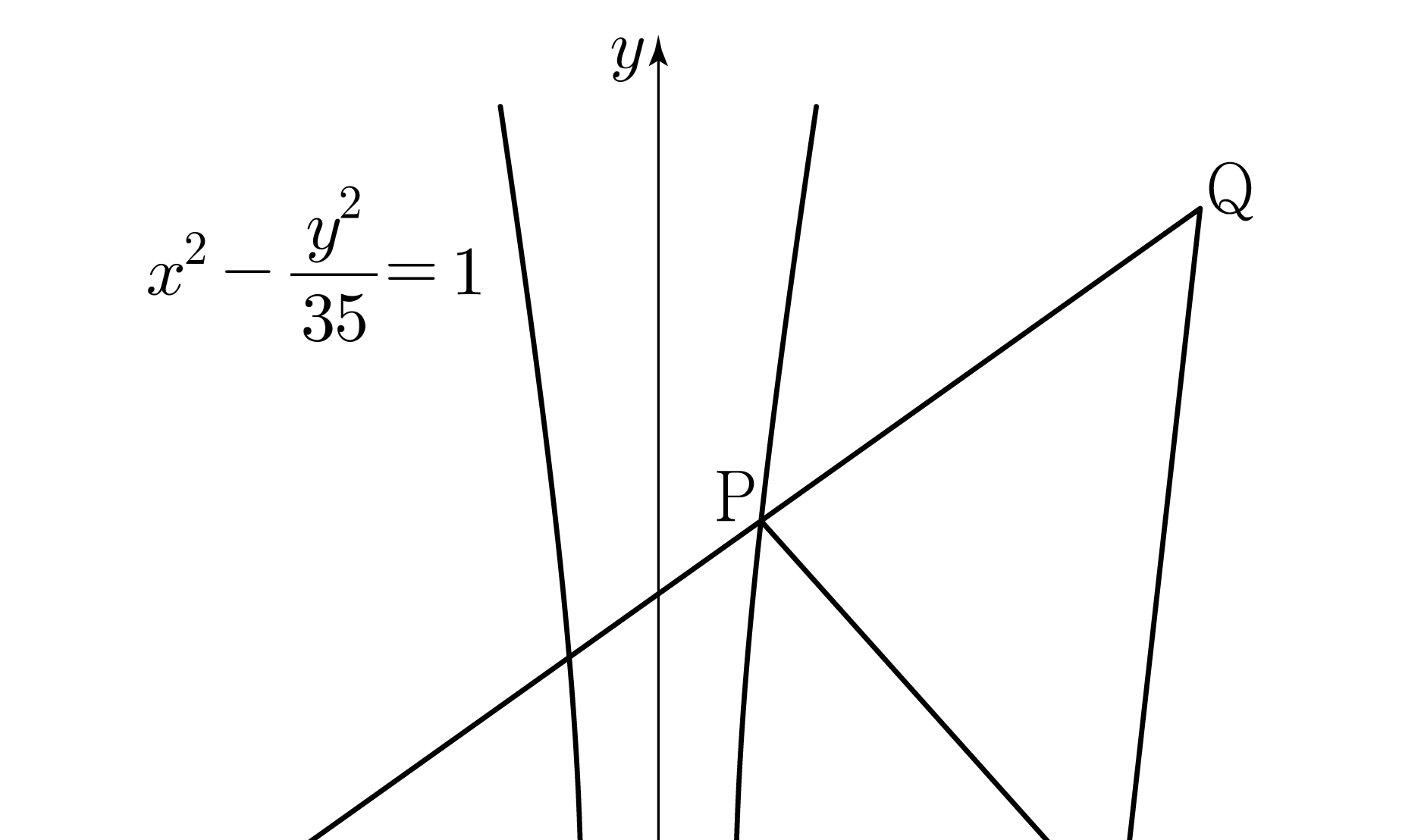
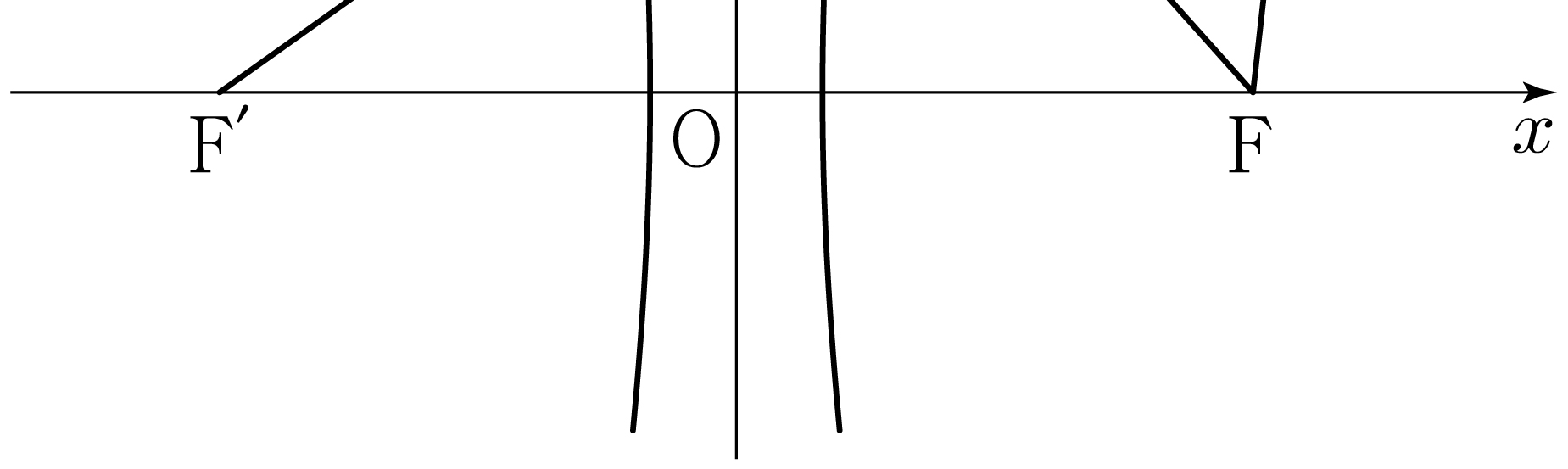
For the origin \(\mathrm{O}\) and point \(\mathrm{P}(3, f(3))\), let \(\mathrm{Q}\) be the point where the line segment \(\mathrm{OP}\) meets the curve \(y=f(x)\). (\(\mathrm{Q} \ne \mathrm{P}\))
Let \(A\) be the area of the region enclosed by the curve \(y=f(x)\), the \(y\)-axis, and the line segment \(\mathrm{OQ}\). Let \(B\) be the area of the region enclosed by the curve \(y=f(x)\) and the line segment \(\mathrm{PQ}\). What is the value of \(B-A\)? [4 points]

\(\dfrac{37}{4}\)
\(\dfrac{39}{4}\)
\(\dfrac{41}{4}\)
\(\dfrac{43}{4}\)
\(\dfrac{45}{4}\)

As the figure shows, let \(\mathrm{D}\) be a point on the edge \(\mathrm{AB}\) of triangle \(\mathrm{ABC}\) such that \(\overline{\mathrm{AD}} : \overline{\mathrm{DB}} = 3 : 2\). Let \(O\) be the circle with center \(\mathrm{A}\) that passes through point \(\mathrm{D}\), and let \(\mathrm{E}\) be the point where circle \(O\) meets the line segment \(\mathrm{AC}\).
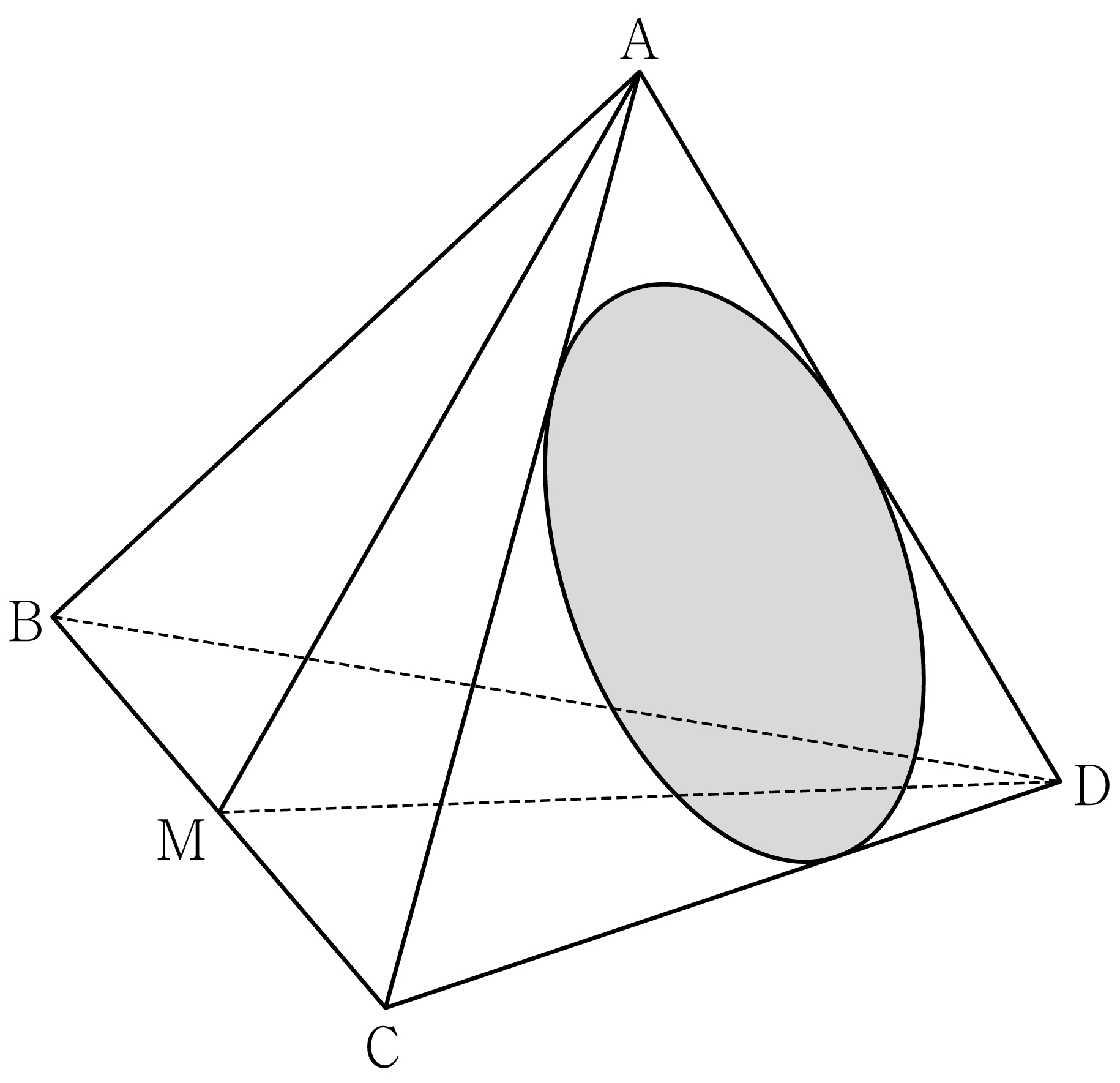
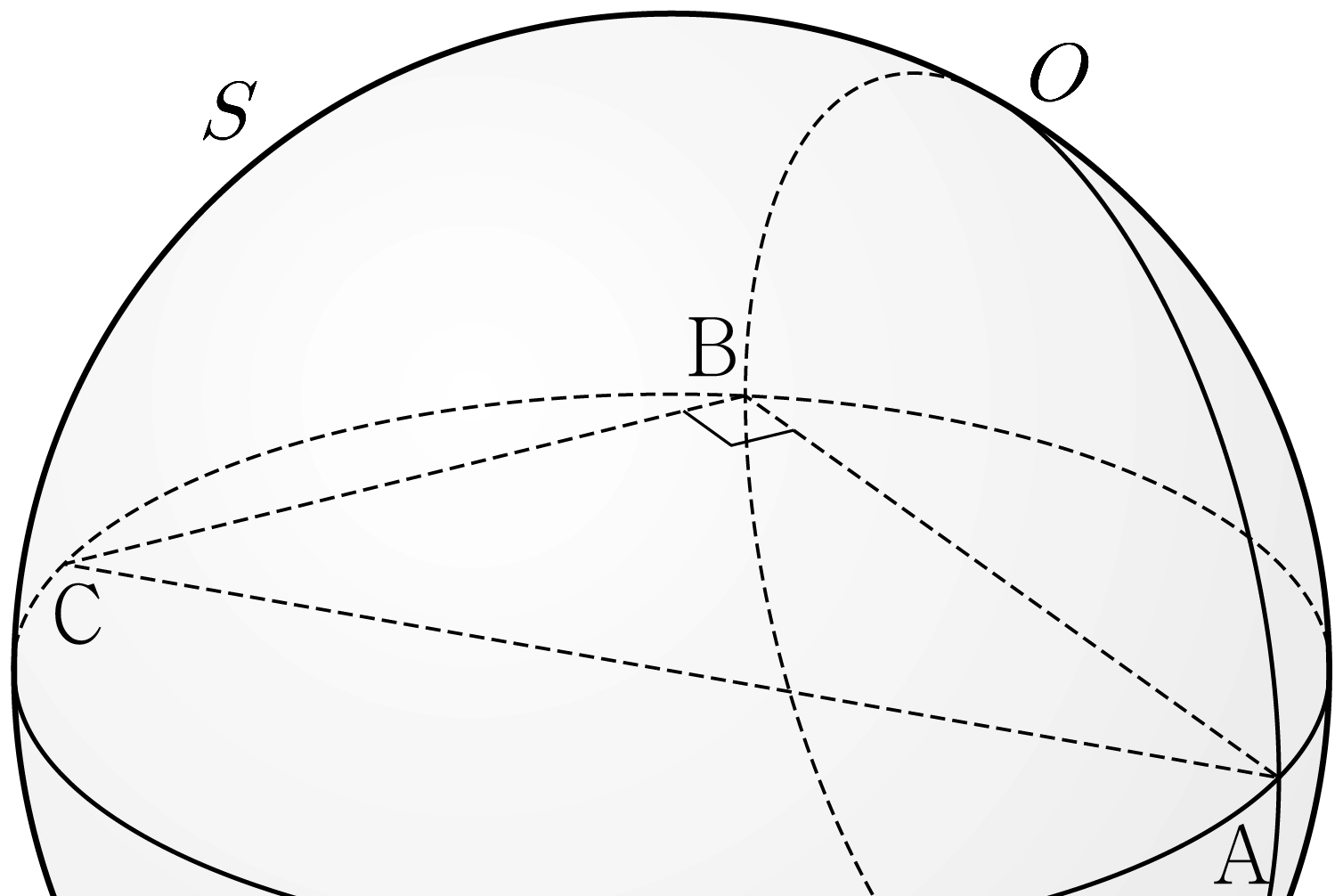
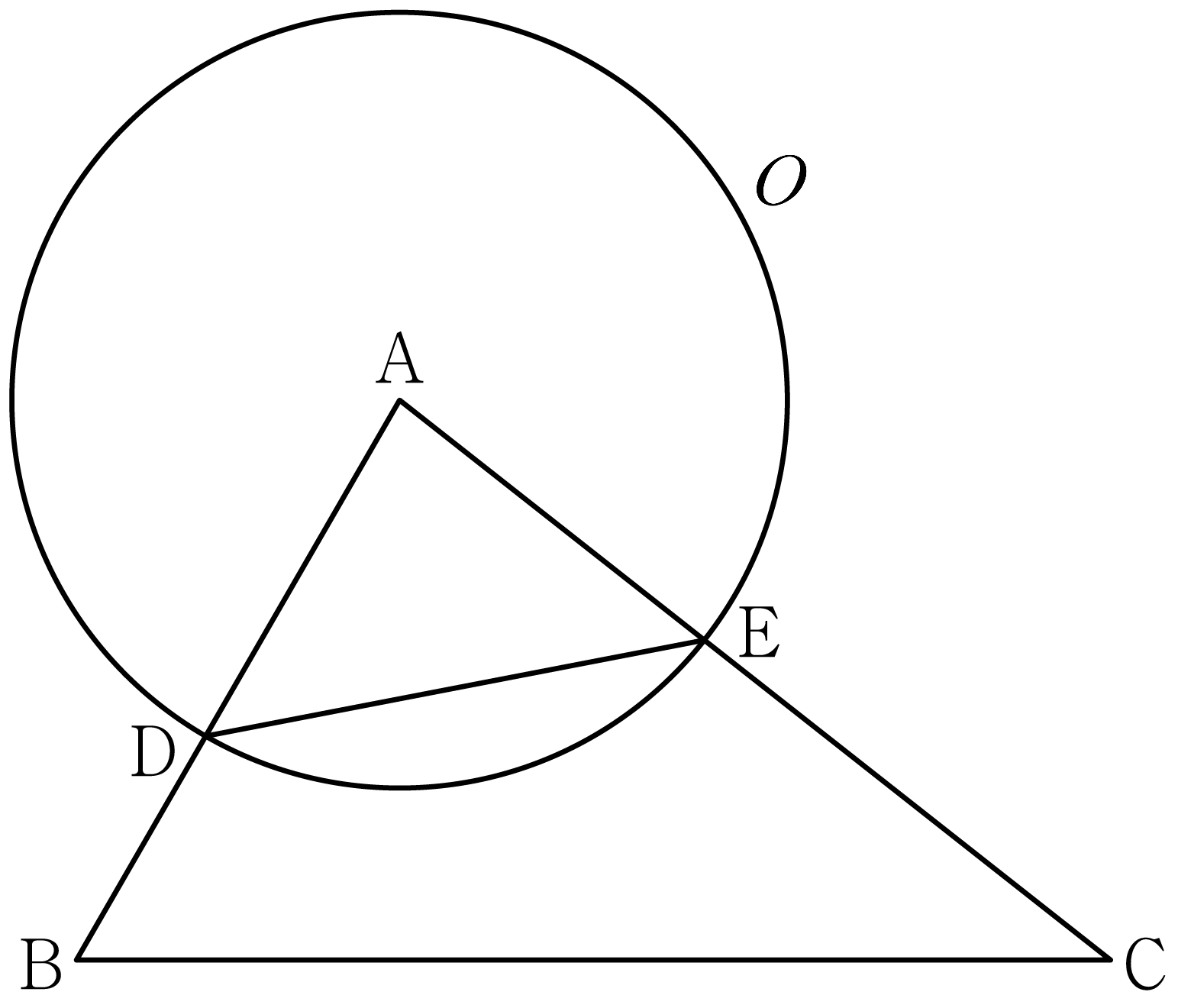
Suppose that \(\sin A : \sin C = 8:5\), and the ratio between the areas of triangle \(\mathrm{ADE}\) and \(\mathrm{ABC}\) is \(9:35\). Suppose that the radius of the circumcircle of triangle \(\mathrm{ABC}\) is \(7\). For all points \(\mathrm{P}\) on circle \(O\), what is the maximum area of triangle \(\mathrm{PBC}\)?
(※ \(\overline{\mathrm{AB}} < \overline{\mathrm{AC}}\)) [4 points]

\(18+15\sqrt{3}\)
\(24+20\sqrt{3}\)
\(30+25\sqrt{3}\)
\(36+30\sqrt{3}\)
\(42+35\sqrt{3}\)

Mathematics

For a constant \(a\) (\(a \ne 3\sqrt{5}\)) and a quadratic function \(f(x)\) with a negative leading coefficient, the function

\(g(x)=\begin{cases} \,x^3+ax^2+15x+7 &\; (x \leq 0) \\\\ \,f(x) &\; (x > 0) \end{cases}\)

satisfies the following condition.

The function \(g(x)\) is differentiable on the set of all real numbers.
The equation \(g'(x) \times g'(x-4) = 0\) has \(4\) distinct real solutions.

What is the value of \(g(-2)+g(2)\)? [4 points]

\(30\)
\(32\)
\(35\)
\(36\)
\(38\)

Short Answer Questions

Compute the value of \(x\) such that \(\log_2(x-3) = \log_4(3x-5)\). [3 points]

Let \(f(x)\) be a polynomial function such that \(f'(x) = 9x^2+4x\,\) and \(\,f(1)=6\). Compute \(f(2)\). [3 points]

Mathematics

Let \(\{a_n\}\) be a sequence such that

\(a_n + a_{n+4} = 12\)

for all positive integers \(n\). Compute \(\displaystyle\sum_{n\;\!=\;\!1}^{16}a_n\). [3 points]

For positive numbers \(a\), let the function \(f(x)\) be

\(f(x)=2x^3-3ax^2-12a^2x\).

Given that \(f(x)\) has a local maximum value of \(\dfrac{7}{27}\), compute \(f(3)\). [3 points]

Let \(k\) be the \(x\)-coordinate of the point where the curve \(y= \!\left(\!\dfrac{1}{5}\!\right)^{\!x-3}\) meets the line \(y=x\). A function \(f(x)\) defined on the set of all real numbers satisfies the following.

For all \(x > k\),
\(f(x)= \!\left(\!\dfrac{1}{5}\!\right)^{\!x-3}\!\) and \(\:f(f(x)) = 3x\).

Compute \(f\!\left(\dfrac{1}{k^3 \times 5^{3k}}\right)\). [4 points]

Mathematics

Let \(a\) and \(b\) be integers such that the function \(f(x)=x^3+ax^2+bx+4\) satisfies the following.

The value of \(\displaystyle\lim_{x\;\!\to\;\!\alpha} \dfrac{f(2x+1)}{f(x)}\) exists for all real numbers \(\alpha\).

Compute the maximum value of \(f(1)\). [4 points]

For all sequences of integers \(\{a_n\}\) that satisfy the following, compute the sum of all values of \(\left|a_1\right|\). [4 points]

For all positive integers \(n\),
\(a_{n+1}=\begin{cases} \,a_n-3 & (\left|a_n\right| \text{ is odd}) \\ \\ \,\dfrac{1}{2}a_n & (a_n=0 \text{ or } \left|a_n\right| \text{ is even}). \end{cases}\)
The minimum value of the positive integer \(m\) such that \(\left|a_m\right|=\left|a_{m+2}\right|\) holds, is \(3\).

2025 College Scholastic Ability Test

Mathematics (Prob. & Stat.)

Multiple Choice Questions

In the expansion of \(\left(x^3+2\right)^{5}\), what is the coefficient of \(x^6\)? [2 points]

\(40\)
\(50\)
\(60\)
\(70\)
\(80\)

Let \(A\) and \(B\) be events such that

\(\mathrm{P}(A \,|\, B) = \mathrm{P}(A) = \dfrac{1}{2}\:\) and \(\:\mathrm{P}(A \cap B) = \dfrac{1}{5}\).

What is the value of \(\mathrm{P}(A \cup B)\)? [3 points]

\(\dfrac{1}{2}\)
\(\dfrac{3}{5}\)
\(\dfrac{7}{10}\)
\(\dfrac{4}{5}\)
\(\dfrac{9}{10}\)

Mathematics (Prob. & Stat.)

A sample of size \(256\) was randomly sampled from a population following the normal distribution \(\mathrm{N}\!\left(m, 2^2\right)\). The \(95\%\) confidence interval for \(m\) computed with this sample is \(a \leq m \leq b\). What is the value of \(b-a\)?
(※ For a random variable \(Z\) that follows the standard normal distribution, suppose \(\mathrm{P}(|Z| \leq 1.96) = 0.95\).) [3 points]

\(0.49\)
\(0.52\)
\(0.55\)
\(0.58\)
\(0.61\)

A survey was conducted on \(16\) students in some class about their preferences between subject \(\mathrm{A}\) and subject \(\mathrm{B}\). Each student selected exactly one of the two subjects. \(9\) students selected subject \(\mathrm{A}\) and 7 students selected subject \(\mathrm{B}\). Suppose \(3\) students are randomly chosen out of the \(16\) students in this survey. What is the probability that at least one of the chosen \(3\) students had selected subject \(\mathrm{B}\)? [3 points]

\(\dfrac{3}{4}\)
\(\dfrac{4}{5}\)
\(\dfrac{17}{20}\)
\(\dfrac{9}{10}\)
\(\dfrac{19}{20}\)

Mathematics (Prob. & Stat.)

There is a sack containing \(5\) cards marked with numbers \(1, 3, 5, 7\) and \(9\) respectively. Let us randomly take out a card from the sack, check the number marked on it, and put it back in the sack. Let us repeat this trial \(3\) times, and let \(\overline{X}\) be the mean of the three checked numbers. Given that \(\mathrm{V}(a \overline{X} + 6) = 24\), what is the value of the positive number \(a\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

For the set \(X=\{1,2,3,4,5,6\}\), what is the number of functions \(f:X\;\!\to\;\!X\) that satisfy the following? [4 points]

\(f(1) \times f(6)\) is a divisor of \(6\).
\(2f(1) \leq f(2) \leq f(3) \leq f(4) \leq f(5) \leq 2f(6)\)

\(166\)
\(171\)
\(176\)
\(181\)
\(186\)

Mathematics (Prob. & Stat.)

Short Answer Questions

A random variable \(X\) following the normal distribution \(\mathrm{N}\!\left(m_1, {\sigma_1}^2\right)\), and a random variable \(Y\) following the normal distribution \(\mathrm{N}\!\left(m_2, {\sigma_2}^2\right)\), satisfy the following.

For all real numbers \(x\),
\(\mathrm{P}(X \leq x) = \mathrm{P}(X \geq 40-x)\) and
\(\mathrm{P}(Y \leq x) = \mathrm{P}(X \leq x+10)\).

Given that the value of \(\mathrm{P}(15\!\leq\!X\!\leq\!20)\!+\!\mathrm{P}(15\!\leq\!Y\!\leq\!20)\), computed with the standard normal table to the right, is \(0.4772\), compute \(m_1 + \sigma_2\).
(※ \(\sigma_1\) and \(\sigma_2\) are positive numbers.) [4 points]

\(z\)	\(\mathrm{P}(0\!\leq\! Z \!\leq\!z)\)
\(0.5\)	\(0.1915\)
\(1.0\)	\(0.3413\)
\(1.5\)	\(0.4332\)
\(2.0\)	\(0.4772\)

There are \(5\) coins on a table in a row. The coins in the \(1\)st and \(2\)nd position are placed with its head facing up, and the rest of the coins are placed with its tail facing up. Let us perform the following trial using these \(5\) coins and a die.

Throw the die once, and let \(k\) be the result.
If \(k \leq 5\), then the coin in the \(k\)th position is turned over once in its position.
If \(k = 6\), then all the coins are turned over once in each of their positions.

After repeating this trial \(3\) times, the probability that all of the \(5\) coins are placed with its head facing up is \(\dfrac{q}{p}\). Compute \(p + q\).
(※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

2025 College Scholastic Ability Test

Mathematics (Calculus)

Multiple Choice Questions

What is the value of \(\displaystyle\lim_{x\,\;\!\to\;\!\,0}\dfrac{3x^2}{\sin^2 x}\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

What is the value of \(\displaystyle\int_{0}^{10} \dfrac{x+2}{x+1} dx\)? [3 points]

\(10 + \ln 5\)
\(10 + \ln 7\)
\(10 + 2\ln 3\)
\(10 + \ln 11\)
\(10 + \ln 13\)

Mathematics (Calculus)

Let \(\{a_n\}\) be a sequence such that \(\displaystyle\lim_{x\;\!\to\;\!\infty} \dfrac{n a_n}{n^2+3} = 1\). What is the value of \(\displaystyle\lim_{n\;\!\to\;\!\infty} \left(\sqrt{{a_n}^2 + n} - a_n\right)\)? [3 points]

\(\dfrac{1}{3}\)
\(\dfrac{1}{2}\)
\(1\)
\(2\)
\(3\)

As the figure shows, there is a \(3\)-dimensional solid where one of its faces is the region enclosed by the curve \(y=\sqrt{\dfrac{x+1}{x(x+\ln x)}}\), the \(x\)-axis, and two lines \(x=1\) and \(x=e\). Suppose a cross section of this solid and any plane perpendicular to the \(x\)-axis is always a square. What is the volume of this solid? [3 points]

\(\ln(e+1)\)
\(\ln(e+2)\)
\(\ln(e+3)\)
\(\ln(2e+1)\)
\(\ln(2e+2)\)

Mathematics (Calculus)

For a cubic function \(f(x)\) with a leading coefficient of \(1\), let the function \(g(x)\) be

\(g(x)=f\left(e^x\right)+e^x\).

Suppose the tangent line to the curve \(y=g(x)\) at point \((0,g(0))\) is the \(x\)-axis, and the function \(g(x)\) has an inverse function \(h(x)\). What is the value of \(h'(8)\)? [3 points]

\(\dfrac{1}{36}\)
\(\dfrac{1}{18}\)
\(\dfrac{1}{12}\)
\(\dfrac{1}{9}\)
\(\dfrac{5}{36}\)

Let \(f(x)\) be a function differentiable on the set of all real numbers, whose derivative \(f'(x)\) is

\(f'(x) = -x + e^{1-x^2}\).

For all positive numbers \(t\), let \(g(t)\) be the area of the region enclosed by the curve \(y=f(x)\), the \(y\)-axis, and the tangent line to the curve \(y=f(x)\) at point \((t, f(t))\). What is the value of \(g(1) + g'(1)\)? [4 points]

\(\dfrac{1}{2}e + \dfrac{1}{2}\)
\(\dfrac{1}{2}e + \dfrac{2}{3}\)
\(\dfrac{1}{2}e + \dfrac{5}{6}\)
\(\dfrac{2}{3}e + \dfrac{1}{2}\)
\(\dfrac{2}{3}e + \dfrac{2}{3}\)

Mathematics (Calculus)

Short Answer Questions

Let \(\{a_n\}\) be a geometric progression such that

\(\displaystyle\sum_{n\;\!=\;\!1}^{\infty}\left(\left|a_n\right| + a_n \right) = \dfrac{40}{3}\) and \(\displaystyle\sum_{n\;\!=\;\!1}^{\infty}\left(\left|a_n\right| - a_n \right) = \dfrac{20}{3}\).

Compute the sum of all positive integers \(m\) for which

\(\displaystyle\lim_{n\;\!\to\;\!\infty} \sum_{k\;\!=\;\!1}^{2n} \left( (-1)^{\begin{array}{c}k\,(k+1) \\\hline 2\end{array}} \times a_{m\,+\,k} \right) > \dfrac{1}{700}\)

is satisfied. [4 points]

For some constants \(a\,(1\leq a\leq 2)\) and \(b\), the function \(f(x)=\sin(ax+b+\sin x)\) satisfies the following.

\(f(0)=0\) and \(f(2\pi) = 2\pi a + b\)
The minimum value of the positive number \(t\) such that \(f'(0)=f'(t)\) holds, is \(4\pi\).

Let \(A\) be the set of all values of \(\alpha\) in the open interval \((0,4\pi)\) such that \(f(x)\) has a local maximum at \(x=\alpha\). Let \(n\) be the number of elements in set \(A\), and let \(\alpha_1\) be the smallest value among the elements in set \(A\). Given that \(n\alpha_1 - ab = \dfrac{q}{p}\pi\), compute \(p+q\).
(※ \(p\) and \(q\) are positive integers that are coprime.) [4 points]

2025 College Scholastic Ability Test

Mathematics (Geometry)

Multiple Choice Questions

Vectors \(\vec{a} = (k,3)\) and \(\vec{b} = (1,2)\) satisfy \(\vec{a} + 3\vec{b} = (6,9)\). What is the value of \(k\)? [2 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

A parabola with vertex \((1,0)\) and directrix \(x=-1\) passes through the point \((3,a)\). What is the value of the positive number \(a\)? [3 points]

\(1\)
\(2\)
\(3\)
\(4\)
\(5\)

Mathematics (Geometry)

Consider two points \(\mathrm{A}(a,b,6)\) and \(\mathrm{B}(-4,-2,c)\). Suppose the point internally dividing the line segment \(\mathrm{AB}\) in the ratio \(3:2\) is on the \(z\)-axis,
and the point externally dividing the line segment \(\mathrm{AB}\) in the ratio \(3:2\) is on the \(xy\)-plane.
What is the value of \(a+b+c\)? [3 points]

\(11\)
\(12\)
\(13\)
\(14\)
\(15\)

For an integer \(n\:(n\geq 2)\), let \(\mathrm{P}\) and \(\mathrm{Q}\) be points where the line \(x= \dfrac{1}{n}\) meets the ellipses

\(C_1: \dfrac{x^2}{2} + y^2 = 1\:\) and \(\:C_2: 2x^2 + \dfrac{y^2}{2} = 1\)

in the \(1\)st quadrant, respectively.
Let \(\alpha\) be the \(x\)-intercept of the tangent line to the ellipse \(C_1\) at point \(\mathrm{P}\),
and let \(\beta\) be the \(x\)-intercept of the tangent line to the ellipse \(C_2\) at point \(\mathrm{Q}\).
What is the number of values \(n\) such that \(6 \leq \alpha-\beta \leq 15\)? [3 points]

\(7\)
\(9\)
\(11\)
\(13\)
\(15\)

Mathematics (Geometry)

Figure shows a tetrahedron \(\mathrm{ABCD}\) with \(\overline{\mathrm{AB}} = 6\) and \(\overline{\mathrm{BC}} = 4\sqrt{5}\). Let \(\mathrm{M}\) be the midpoint of the line segment \(\mathrm{BC}\). Suppose triangle \(\mathrm{AMD}\) is an equilateral triangle, and line \(\mathrm{BC}\) is perpendicular to plane \(\mathrm{AMD}\). Consider the incircle of triangle \(\mathrm{ACD}\). What is the area of the projection of this circle onto plane \(\mathrm{BCD}\)? [3 points]

\(\dfrac{\sqrt{10}}{4} \pi\)
\(\dfrac{\sqrt{10}}{6} \pi\)
\(\dfrac{\sqrt{10}}{8} \pi\)
\(\dfrac{\sqrt{10}}{10} \pi\)
\(\dfrac{\sqrt{10}}{12} \pi\)

Consider a right triangle \(\mathrm{ABC}\) in \(3\)-dimensional space, with \(\overline{\mathrm{AB}}=8\), \(\overline{\mathrm{BC}}=6\) and \(\angle \mathrm{ABC} = \dfrac{\pi}{2}\).
Let \(S\) be a sphere with the line segment \(\mathrm{AC}\) as a diameter. Let the circle \(O\) be the intersection of sphere \(S\) and a plane which contains line \(\mathrm{AB}\) and is perpendicular to plane \(\mathrm{ABC}\).
Let \(\mathrm{P}\) and \(\mathrm{Q}\) be two distinct points on circle \(O\) whose distance to line \(\mathrm{AC}\) is \(4\). What is the length of the line segment \(\mathrm{PQ}\)? [4 points]

\(\sqrt{43}\)
\(\sqrt{47}\)
\(\sqrt{51}\)
\(\sqrt{55}\)
\(\sqrt{59}\)

Mathematics (Geometry)

Short Answer Questions

Consider the hyperbola \(x^2- \dfrac{y^2}{35}=1\), with foci \(\mathrm{F}(c, 0)\) and \(\mathrm{F'}(-c, 0)\) \((c>0)\). Let \(\mathrm{P}\) be a point on this hyperbola in the \(1\)st quadrant, and let \(\mathrm{Q}\) be a point on line \(\mathrm{PF'}\) such that \(\overline{\mathrm{PQ}}= \overline{\mathrm{PF}}\). Given that triangles \(\mathrm{QF'F}\) and \(\mathrm{FF'P}\) are similar, the area of the triangle \(\mathrm{PFQ}\) is \(\dfrac{q}{p} \sqrt{5}\). Compute \(p+q\).
(※ Suppose \(\overline{\mathrm{PF'}} < \overline{\mathrm{QF'}}\). Suppose \(p\) and \(q\) are positive integers that are coprime.) [4 points]

Consider a square \(\mathrm{ABCD}\) on the \(xy\)-plane with side lengths of \(4\). Let the shape \(S\) be the set of all points \(\mathrm{X}\) such that

\(\big|\, \overrightarrow{\mathrm{XB}} + \overrightarrow{\mathrm{XC}} \,\big| = \big|\, \overrightarrow{\mathrm{XB}} - \overrightarrow{\mathrm{XC}} \,\big|\).

For a point \(\mathrm{P}\) on shape \(S\), let \(\mathrm{Q}\) be a point such that

\(4 \overrightarrow{\mathrm{PQ}} = \overrightarrow{\mathrm{PB}} + 2 \overrightarrow{\mathrm{PD}}\).

Let \(M\) and \(m\) be the maximum and minimum value of \(\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{AQ}}\), respectively. Compute \(M \times m\). [4 points]